Khi x thay đổi trong khoảng 5 π 4 , 7 π 4 thì y = sin x lấy mọi giá trị thuộc:
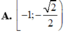
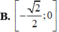
![]()
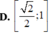
Đặt một điện áp xoay chiều u = U 0 cos ( 100 π t + φ ) (V) vào hai đầu một đoạn mạch gồm R, L, C mắc nối tiếp (L là cuộn cảm thuần). Biết C = 10 - 4 / π (F); R không thay đổi, L thay đổi được. Khi L = L 1 = 2 / π (H) thì biểu thức của cường độ dòng điện trong mạch là i = I 1 √ 2 cos ( 100 π t – π / 12 ) (A). Khi L = L 2 = 4 / π (H) thì biểu thức của cường độ dòng điện trong mạch là i = I 2 √ 2 cos ( 100 π t – π / 4 ) (A). Điện trở R có giá trị là:
A. 100 Ω
B. 100 √ 2 Ω
C. 200 Ω
D. 100 √ 3 Ω
Đặt một điện áp xoay chiều u = U0cos(100πt + φ) (V) vào hai đầu một đoạn mạch gồm R, L, C mắc nối tiếp (L là cuộn cảm thuần). Biết C = 10-4/π (F); R không thay đổi, L thay đổi được. Khi L = L1 = 2/π (H) thì biểu thức của cường độ dòng điện trong mạch là i = I1√2cos(100πt – π/12) (A). Khi L = L2 = 4/π (H) thì biểu thức của cường độ dòng điện trong mạch là i = I2√2cos(100πt – π/4) (A). Điện trở R có giá trị là
A. 100 Ω
B. 100√2 Ω
C. 100√3 Ω
D. 200 Ω
Khi x thay đổi trong khoảng 2 π 3 ; 7 π 3 thì hàm y = cosx lấy mọi giá trị thuộc khoảng
A. 0 ; 1 2
B. 0 ; 1
C. 1 2 ; 1
D. 0 ; 1 2
Khi x thay đổi trong khoảng 5 π 7 ; 7 π 4 thì y = sinx có giá trị thuộc
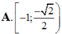
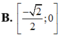
![]()
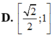
Khi x thay đổi trong khoảng 5 π 4 ; 7 π 4 thì y = s inx lấy mọi giá trị thuộc:
A. − 1 ; − 2 2
B. − 2 2 ; 0
C. − 1 ; 1
D. 2 2 ; 1
Đáp án A
Vì 270 0 ∈ 225 0 ; 315 0 sin 270 0 = − 1 sin 225 0 = sin 315 0 = − 2 2 ⇒ − 1 ≤ sin x < − 2 2 h a y y ∈ − 1 ; − 2 2
(Cách khác: Hs kiểm tra trên MTBT bằng cách vào Mode 7 vẫn đc kết quả đáp án A )
Một đoạn mạch nối tiếp gồm điện trở R có thể thay đổi được, tụ điện C=125/π μF và cuộn dây thuần cảm L=2/π H. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều u = 150 2 cos 100 π t V. Thay đổi R để công suất tiêu thụ trong mạch bằng 90 W. Khi đó R có hai giá trị R 1 và R2 bằng :
A. R 1 = 190 Ω v à R 2 = 160 Ω .
B. R 1 = 80 Ω v à R 2 = 60 Ω .
C. R 1 = 90 Ω v à R 2 = 160 Ω
D. R 1 = 60 Ω v à R 2 = 160 Ω .
Ta có R 1 v à R 2 là hai nghiệm của phương trình R 2 − U 2 P R + Z L − Z C 2 = 0 ⇔ R 2 – 250 R + 14400 = 0
→ R 1 = 160 Ω v à R 2 = 90 Ω .
Đáp án C
Đoạn mạch RLC đặt dưới điện áp xoay chiều ổn định có tần số f thay đổi được. Khi tần số là f 1 và khi tần số là f 2 thì pha ban đầu của dòng điện qua mạch là -π/6 và π/3 còn cường độ hiệu dụng không thay đổi. Tính hệ số công suất mạch khi tần số là f 1 ?
A. 0,5.
B. 0,71.
C. 0,87.
D. 0,6
Đoạn mạch RLC đặt dưới điện áp xoay chiều ổn định có tần số f thay đổi được. Khi tần số là f1 và khi tần số là f2 thì pha ban đầu của dòng điện qua mạch là -π/6 và π/3 còn cường độ hiệu dụng không thay đổi. Tính hệ số công suất mạch khi tần số là f1?
A. 0,5.
B. 0,71.
C. 0,87.
D. 0,6.
Trong các khoảng sau, m thuộc khoảng nào để phương trình sin^2 x-(2m+1) sin x.cos x + 2m cos^2 x = 0 có nghiệm thuộc khoảng (π/4 ; π/3)?
\(sin^2x-2m.sinx.cosx-sinx.cosx+2mcos^2x=0\)
\(\Leftrightarrow sinx\left(sinx-cosx\right)-2mcosx\left(sinx-cosx\right)=0\)
\(\Leftrightarrow\left(sinx-cosx\right)\left(sinx-2m.cosx\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=cosx\\sinx=2m.cosx\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}tanx=1\\tanx=2m\end{matrix}\right.\)
Do \(tanx=1\) ko có nghiệm đã cho nên \(tanx=2m\) phải có nghiệm trên khoảng đã cho
\(\Rightarrow tan\left(\dfrac{\pi}{4}\right)< 2m< tan\left(\dfrac{\pi}{3}\right)\)
\(\Rightarrow1< 2m< \sqrt[]{3}\)
\(\Rightarrow m\in\left(\dfrac{1}{2};\dfrac{\sqrt{3}}{2}\right)\) (hoặc có thể 1 đáp án là tập con của tập này cũng được)