Trong các dãy số u n sau đây, dãy số nào là cấp số nhân ?
A. u n = 3 n
B. u n = 2 n
C. u n = 1 n
D. u n = 2 n + 1
Những câu hỏi liên quan
Trong các dãy số sau đây dãy số nào là cấp số nhân? A. Dãy số
u
n
, xác định bởi hệ :
u
1
1
u
n
u...
Đọc tiếp
Trong các dãy số sau đây dãy số nào là cấp số nhân?
A. Dãy số u n , xác định bởi hệ : u 1 = 1 u n = u n − 1 + 2 n ∈ ℕ * : n ≥ 2
B. Dãy số các số tự nhiên 1; 2; 3....
C. Dãy số u n , xác định bởi công thức u n = 3 n + 1 v ớ i n ∈ ℕ *
D. Dãy số − 2 ; 2 ; − 2 ; 2 ; ... ; − 2 ; 2 ; − 2 ; 2 ; ...
Trong các dãy số sau đây dãy số nào là cấp số nhân? A. Dãy số -2,2,-2,2,...,-2,2,-2,2... B. Dãy số các số tự nhiên 1, 2, 3,... C. Dãy số
u
n
, xác định bởi công thức:
u
n
3
n
+
1
v
ớ
i
n
∈
N
*...
Đọc tiếp
Trong các dãy số sau đây dãy số nào là cấp số nhân?
A. Dãy số -2,2,-2,2,...,-2,2,-2,2...
B. Dãy số các số tự nhiên 1, 2, 3,...
C. Dãy số u n , xác định bởi công thức:
u n = 3 n + 1 v ớ i n ∈ N * với n ∈ N *
D. Dãy số u n , xác định bởi hệ:
u 1 = 1 u n = u n - 1 + 2 ( n ∈ N * : n ≥ 2 )
Trong các dãy số
u
n
sau đây, dãy số nào là cấp số nhân? A.
u
n
3
n
B.
u
n
2
n
C.
u
n
1
n
D.
u...
Đọc tiếp
Trong các dãy số u n sau đây, dãy số nào là cấp số nhân?
A. u n = 3 n
B. u n = 2 n
C. u n = 1 n
D. u n = 2 n + 1
trang 60 SGK Toán 11 tập 1 - Chân trời sáng tạo
17 tháng 7 2023 lúc 12:29
Trong các dãy số sau đây, dãy số nào là cấp số nhân?
a) \({u_n} = 3{\left( { - 2} \right)^n}\);
b) \({u_n} = {\left( { - 1} \right)^{n + 1}}{.7^n}\);
c) \(\left\{ \begin{array}{l}{u_1} = 1\\{u_{n + 1}} = 2{u_n} + 3\end{array} \right.\).
a) Ta có: \({u_{n + 1}} = 3{\left( { - 2} \right)^{n + 1}}\)
Xét thương: \(\frac{{{u_{n + 1}}}}{{{u_n}}} = \frac{{3{{\left( { - 2} \right)}^{n + 1}}}}{{3{{\left( { - 2} \right)}^n}}} = \frac{{3{{\left( { - 2} \right)}^n}.\left( { - 2} \right)}}{{3{{\left( { - 2} \right)}^n}}} = - 2\)
Vậy dãy số là cấp số nhân có công bội \(q = - 2\).
b) Ta có: \({u_{n + 1}} = {\left( { - 1} \right)^{\left( {n + 1} \right) + 1}}{.7^{n + 1}} = {\left( { - 1} \right)^{n + 2}}{.7^{n + 1}}\)
Xét thương: \(\frac{{{u_{n + 1}}}}{{{u_n}}} = \frac{{{{\left( { - 1} \right)}^{n + 2}}{{.7}^{n + 1}}}}{{{{\left( { - 1} \right)}^{n + 1}}{{.7}^n}}} = \frac{{{{\left( { - 1} \right)}^{n + 1}}.\left( { - 1} \right){{.7}^n}.7}}{{{{\left( { - 1} \right)}^{n + 1}}{{.7}^n}}} = - 7\)
Vậy dãy số là cấp số nhân có công bội \(q = - 7\).
c) Ta có: \({u_1} = 1;{u_2} = 2{u_1} + 3 = 2.1 + 3 = 5;{u_3} = 2{u_2} + 3 = 2.5 + 3 = 13\)
Vì \(\frac{{{u_2}}}{{{u_1}}} \ne \frac{{{u_3}}}{{{u_2}}}\) nên dãy số không là cấp số nhân.
Đúng 0
Bình luận (0)
Trong các dãy số dưới đây, dãy số nào là cấp số nhân? A. Dãy số
x
n
, với
x
n
n
2
B. Dãy số
y
n
với
y
n
5...
Đọc tiếp
Trong các dãy số dưới đây, dãy số nào là cấp số nhân?
A. Dãy số x n , với x n = n 2
B. Dãy số y n với y n = 5 2 n - 3
C. Dãy số z n với z n = 2 n
D. Dãy số w n với w n = 3 n + 1 3 n + 1
Trong các dãy số dưới đây, dãy số nào không là cấp số nhân lùi vô hạn? A. Dãy số
1
3
;
1
9
;
1
27
;
...
,
1
3
n
;
...
B.
1
;
−
1
2...
Đọc tiếp
Trong các dãy số dưới đây, dãy số nào không là cấp số nhân lùi vô hạn?
A. Dãy số 1 3 ; 1 9 ; 1 27 ; ... , 1 3 n ; ...
B. 1 ; − 1 2 ; 1 4 ; − 1 8 ; 1 16 ; ... ; − 1 2 n − 1 ; ...
C. Dãy số 3 3 ; 4 9 ; 8 27 ; ... , 2 3 2 ; ...
D. 3 2 ; 9 4 ; 29 8 ; ... ; 3 2 n ; ...
Trong các dãy số sau, dãy số nào là cấp số nhân? A.
u
n
5
n
+
3
,
n
≥
1
B.
u
n
4
+
3
n
,
n
≥
1
C.
u
1...
Đọc tiếp
Trong các dãy số sau, dãy số nào là cấp số nhân?
A. u n = 5 n + 3 , n ≥ 1
B. u n = 4 + 3 n , n ≥ 1
C. u 1 = 3 u n + 1 = 7 u n , n ≥ 1
D. u 1 = 2 u n + 1 = u 2 n , n ≥ 1
Trong các dãy số sau, dãy số nào là một cấp số nhân.
A. 1;-2;4;-8;-16;-32
B. 1;3;9;17;81;243
C. 2;4;6;8;12;16;32;63
D. 4;2;1;0,5;-0,25
Chọn B.
- Theo tính chất của cấp số nhân: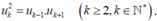 
+ Đáp án A: ( - 8 ) 2 ≠ - 4 . 16 nên A sai.
+ Đáp án C: 6 2 ≠ 4 . 8 nên C sai.
+ Đáp án D: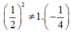 
nên D sai.
Đúng 0
Bình luận (0)
Trong các dãy số sau, dãy số nào là một cấp số nhân? A.
128
;
−
64
;
32
;
−
16
;
8
;
...
B.
2
;
2
;
4
;
4
2
;
....
C.
5
;
6
;...
Đọc tiếp
Trong các dãy số sau, dãy số nào là một cấp số nhân?
A. 128 ; − 64 ; 32 ; − 16 ; 8 ; ...
B. 2 ; 2 ; 4 ; 4 2 ; ....
C. 5 ; 6 ; 7 ; 8 ; ...
D. 1 π ; 1 π 2 ; 1 π 4 ; 1 π 6 ; ⋯
Dãy (un) là cấp số nhân
⇔ u n = q u n − 1 n ∈ ℕ * ⇔ u 2 u 1 = u 3 u 2 = u 4 u 3 = ⋯ = q u n = 0 , q là công bội.
Xét đáp án A: 128 ; − 64 ; 32 ; − 16 ; 8 ; ... ⇒ u 2 u 1 = − 1 2 = u 3 u 2 = u 4 u 3 ⇒ Chọn A.
Xét đáp án B: 2 ; 2 ; 4 ; 4 2 ; .... ⇒ u 2 u 1 = 1 2 = 2 = u 3 u 2 ⇒ loại B.
Tương tự, ta cũng loại các đáp án C, D.
Chọn đáp án A.
Đúng 0
Bình luận (0)