Tính bán kính R mặt cầu ngoại tiếp tứ diện đều ABCD cạnh a 2
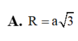
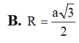
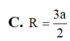
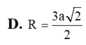
Tính bán kính R mặt cầu ngoại tiếp tứ diện đều ABCD cạnh a 2
A. R = a 3
B. R = a 3 2
C. R = 3 a 2
D. R = 3 a 2 2
Đáp án B
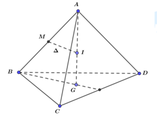
Gọi G là trọng tâm Δ B C D , ta có A G ⊥ B C D nên AG là trục của Δ B C D ,
Gọi M là trung điểm của AB. Qua M dựng đường thẳng Δ ⊥ A B , gọi I = Δ ∩ A G
Do đó mặt cầu ngoại tiếp tứ diện ABCD có tâm là I và bán kính R = I A
Ta có Δ A M I , Δ A G B là hai tam giác vuông đồng dạng nên I A A B = A M A G ⇒ A I = A B . A M A G
Do A B = a 2 , A M = a 2 2 , A G = a 2 2 − 2 3 . a 2 . 3 2 2 = 2 a 3 3
Khi đó R = A I = a 2 . a 2 2 2 a 3 3 = a 3 2
Cách 2: Áp sụng công thức giải nhanh R = A B 2 2 S G = a 3 2
II. Tự luận ( 4 điểm)
Tính bán kính của mặt cầu ngoại tiếp hình tứ diện ABCD đều cạnh a.
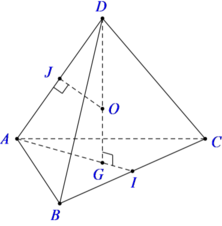
Gọi I là trung điểm cạnh BC, G là trọng tâm của tam giác ABC.

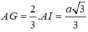 và DG là trục của tam giác ABC.
và DG là trục của tam giác ABC.
Trong mp (DAG), kẻ trung trực của DA cắt DG tại O thì: OD = OA = OB = OC nên O chính là tâm mặt cầu ngoại tiếp tứ diện ABCD.
Bán kính R của mặt cầu bằng độ dài đoạn OD.
Trong tam giác ADG vuông tại G, ta có:
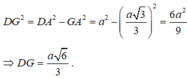
Mặt khác, tam giác DJO đồng dạng tam giác DGA nên:
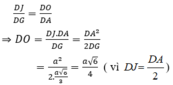
Vậy bán kính của mặt cầu ngoại tiếp hình tứ diện ABCD đều cạnh a là R = a 6 4
Gọi r , R lần lượt là bán kính mặt cầu nội tiếp và ngoại tiếp tứ diện đều ABCD. Tính tỉ số R r ?
![]()
![]()
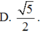
Tứ diện ABCD là tứ diện đều nội tiếp trong mặt cầu bán kính R. Tính độ dài của cạnh tứ diện đều theo R
A. R 2
B. R 3
C. 2 R 2 3
D. R 6 2
Đáp án C
Đặt AB = x, M, N lần lượt là trung điểm AB, CD, I là trung điểm MN thì I là tâm mặt cầu, có
![]()
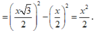
![]()
![]()
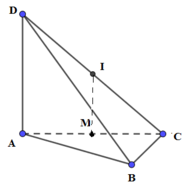
Cho tứ diện ABCD có DA vuông góc với (ABC) và AD = a, AC = 2a; cạnh BC vuông góc với cạnh AB. Tính bán kính r của mặt cầu ngoại tiếp tứ diện ABCD.
A. r = a 5
B. r = a 3 2
C. r = a
D. r = a 5 2
Đáp án D
Phương pháp:
+) Xác định tâm mặt cầu ngoại tiếp khối tứ diện là điểm cách đều tất cả các đỉnh của tứ diện.
+) Áp dụng định lí Pytago tính bán kính mặt cầu ngoại tiếp tứ diện.
Cách giải:
Tam giác ABC vuông tại B, M là trung điểm của AC ⇒ M là tâm đường tròn ngoại tiếp tam giác ABC
Gọi I là trung điểm của CD ⇒ IC = ID(1)
Ta có: IM là đường trung bình của tam giác ACD ⇒ IM // AD
Mà AD ⊥ (ABC) ⇒ IM ⊥ (ABC)
Do đó, IM là trục đường tròn ngoại tiếp tam giác ABC
⇒ IA = IB = IC(2)
Từ (1), (2) ⇒ IA = IB = IC = ID ⇒ I là tâm mặt cầu ngoại tiếp tứ diện ABCD, bán kính mặt cầu:
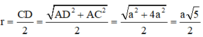
Cho tứ diện ABCD có AB = 4a, CD = 6a, các cạnh còn lại đều bằng a 22 . Tính bán kính của mặt cầu ngoại tiếp tứ diện ABCD.
A. 5 a 2
B. 3a
C. a 85 3
D. a 79 3
Cho tứ diện ABCD có AB =4a, CD= 6a, các cạnh còn lại đều bằng a 22 .Tính bán kính của mặt cầu ngoại tiếp tứ diện ABCD.
A. 5 a 2
B. 3a
C. a 85 3
D. a 79 3
Đáp án C.
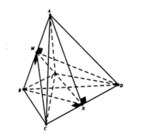
Gọi M, N lần lượt là trung điểm của AB và CD

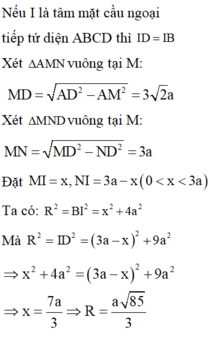
Cho tứ diện ABCD có DA vuông góc với mặt phẳng (ABC) và AD = a, AC = 2a. cạnh BC vuông góc với AB. Tính bán kính r của mặt cầu ngoại tiếp tứ diện ABCD.
A. r = a 5
B. r = a 3 2
C. r = a
D. r = a 5 2
Cho tứ diện A B C D có DA vuông góc với mặt phẳng ( A B C ) và A D = a , A C = 2 a , cạnh BC vuông góc với AB. Tính bán kính r của mặt cầu ngoại tiếp tứ diện A B C D .
![]()
![]()