Thể tích V của khối chóp tứ giác đều có chiều cao h và bán kính mặt cầu nội tiếp r (h>2r>0)
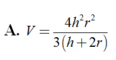
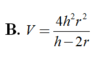
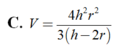
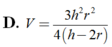
Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng 9, tính thể tích V của khối chóp có thể tích lớn nhất.
A. V = 144
B. V = 576 2
C. V = 576
D. V = 144 6
Đáp án C
Gọi chiều cao của hình chóp là 9 + x , x ≥ 0 , cạnh của hình chóp là a , a ≤ 9 2
Diện tích đáy của hình chóp là: V = 1 3 .2 81 − x 2 9 + x = 2 3 9 − x = 2 3 9 − x 9 + x 9 + x
= 1 3 18 − 2 x 9 + x 9 + x = 1 3 ≤ 1 3 18 − 2 x + 9 + x + 9 + x 3 3 = 1 3 .12 3 = 576
Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng 9, tính thể tích V của khối chóp có thể tích lớn nhất.
A. V = 144
B. V = 576 2
C. V = 576
D. V = 144 6
Cho mặt cầu (S) có bán kính R cố định. Gọi (H) là hình chóp tứ giác đều có thể tích lớn nhất nội tiếp trong (S). Tìm theo R độ dài cạnh đáy (H).
A. 4 R 3
B. 2 R 3
C. R 3
D. R
Cho mặt cầu (S) có bán kính R cố định. Gọi (H) là hình chóp tứ giác đều có thể tích lớn nhất nội tiếp trong (S). Tìm theo R độ dài cạnh đáy (H).
A. 4 R 3
B. 2 R 3
C. R 3
D.R
Đáp án A

Ký hiệu như hình vẽ. Đặt A B = B C = C D = D A = a ; S O = h
Suy ra S B = a 2 2 + h 2
Gọi M là trung điểm của SB
Trong (SBD) kẻ trung trực của SB cắt SO tại I
Vậy I là tâm mặt cầu ngoại tiếp khối chóp S.ABCD. Suy ra I S = R .
Hai tam giác vuông SMI và SOB đồng dạng ⇒ S I S B = S M S O ⇒ R = a 2 + 2 h 2 4 h với 0 < h < 2 R . Suy ra a 2 = 2 h 2 R − h .
Thể tích V của khối chóp là:
V = 1 3 a 2 h = 1 3 2 h 2 2 R − h = 8 3 h 2 h 2 2 R − h ≤ 8 3 h 2 + h 2 + 2 R − h 3 3 = 64 R 3 81
Vậy GTLN của V bằng 64 R 3 81 đạt được khi h 2 = 2 R − h ⇔ h = 4 R 3
Suy ra a = 4 R 3 .
Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng 9, tính thể tích của khối chóp có thể tích lớn nhất.
A. V=144
B.V=576 2
C.V=144 6
D.V=576
Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng 9, tính thể tích 𝑉 của khối chóp có thể tích lớn nhất.
A. V=144
B. V=576
C. V = 576 2
D. V = 144 6

Đáp án B
Ta có: R = S A 2 2 S O = 9
Suy ra S O 2 + O A 2 S O = 18
Mặt khác V S . A B C D = 1 3 S O . S A B C D = 1 3 S O . A C 2 2 = 2 3 S O . O A 2
= 2 3 S O . 18 S O − S O 2 . đặt S O = t 0 < t < 18 , xét hàm số
f t = 2 3 t 2 18 − t = 8 3 . t 2 . t 2 18 − t ≤ 8 3 t + 18 − t 3 3 = 576
Hình chóp tứ giác đều nội tiếp trong một mặt cầu bán kính R=1 có thể tích V m a x (hình vẽ)
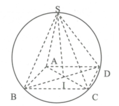
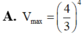
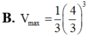
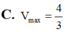
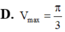
Trong tất cả các hình chóp tứ giác đều nội tiếp hình cầu có bán kính bằng 9. Tính thể tích V của khối chóp có thể tích lớn nhất.
![]()
![]()
![]()
![]()
Trong tất cả các hình chóp tứ giác đều nội tiếp hình cầu có bán kính bằng 9. Tính thể tích V của khối chóp có thể tích lớn nhất.
A. 144 2
B. 144.
C. 576 2
D. 576.