Cho x, y là các số thực lớn hơn 1 thỏa mãn x2 + 9y2 = 6xy. Tính M = 1 + log 12 x + log 12 y 2 . log 12 ( x + 3 y ) .
A. M = 1.
B. M = 1 + log 12 3 y log 12 6 .
C. M = 2.
D. M = log12 6.
Những câu hỏi liên quan
Cho x, y là các số thực lớn hơn 1 thỏa mãn
x
2
+
9
y
2
6
x
y
.
Tính
M
1
+
log
12
x
+
log
12
y
2....
Đọc tiếp
Cho x, y là các số thực lớn hơn 1 thỏa mãn x 2 + 9 y 2 = 6 x y . Tính M = 1 + log 12 x + log 12 y 2. log 12 x + 3 y .
A. M = 1.
B. M = 1 + log 12 3 y log 12 6 .
C. M = 2 .
D. M = log 12 6.
Cho x; y là các số thực lớn hơn thoả mãn x2 + 9y2 6xy . Tính
M
1
+
log
12
x
+
log
12
y
2
log
12
x
+...
Đọc tiếp
Cho x; y là các số thực lớn hơn thoả mãn x2 + 9y2 = 6xy . Tính M = 1 + log 12 x + log 12 y 2 log 12 x + 3 y
A. M = 1/4.
B. M = 1.
C. M = 1/2.
D. M = 1/3.
Chọn B.
Ta có x2 + 9y2 = 6xy tương đương (x - 3y) 2 = 0 hay x = 3y.
Khi đó 
Đúng 0
Bình luận (0)
Giả sử a,b là các số thực sao cho
x
3
+
y
3
a
10
3
x
+
b
10
2
x
đúng với mọi các số thực dương x, y, z thỏa mãn
log
(
x
+
y...
Đọc tiếp
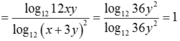
Giả sử a,b là các số thực sao cho x 3 + y 3 = a 10 3 x + b 10 2 x đúng với mọi các số thực dương x, y, z thỏa mãn log ( x + y ) = z và log ( x 2 + y 2 ) = z + 1 . Giá trị của a+b bằng
A. -31/2
B. -25/2
C. 31/2
D. 29/2
11 tháng 3 2022 lúc 8:58
Cho x, y là các số thực lớn hơn 1 thoả mãn \(x^2+9y^2=6xy\) . Chứng minh:
\(\dfrac{1+log_{12}x+log_{12}y}{2log_{12}\left(x+3y\right)}=1\)
Cho hàm số
y
ln
(
2
x
-
a
)
-
2
m
ln
(
2
x
-
a
)
+...
Đọc tiếp
Cho hàm số y = ln ( 2 x - a ) - 2 m ln ( 2 x - a ) + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + . . . + log . . . 2 ( x 2 + a 2 ) - ( 2 n + 1 - 1 ) ( log 2 x a + 1 ) = 0
(với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thoả mãn m a x [ 1 ; e 2 ] y = 1 . Số phần tử của S là
A. 0
B. 1
C. 2
D. Vô số
Giả sử a, b là các số thực sao cho x3 + y3 a.103x + b.102x đúng với mọi số thực dương x, y, z thỏa mãn log (x + y) z và log(x2 + y2) z + 1. Giá trị của a+b bằng: A.
-
31
2
B.
-
25
2
C.
31
2
D.
29
2
Đọc tiếp
Giả sử a, b là các số thực sao cho x3 + y3 = a.103x + b.102x đúng với mọi số thực dương x, y, z thỏa mãn log (x + y) = z và log(x2 + y2) = z + 1. Giá trị của a+b bằng:
A. - 31 2
B. - 25 2
C. 31 2
D. 29 2
Đáp án D.
Ta có
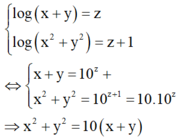
Khi đó
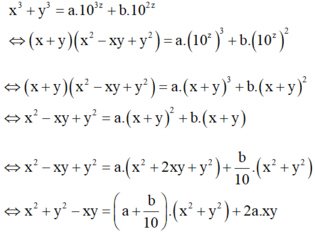
Đồng nhất hệ số, ta được
Đúng 0
Bình luận (0)
Cho x, y là các số thực thỏa mãn
x
+
y
x
-
1
+
2
y
+
2
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của
P
x
2
+
y
2
+
2
(
x
+
1
)
(
y
+
1
)
+
8
4
-
x
-...
Đọc tiếp
Cho x, y là các số thực thỏa mãn x + y = x - 1 + 2 y + 2 Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của P = x 2 + y 2 + 2 ( x + 1 ) ( y + 1 ) + 8 4 - x - y Tính giá trị M + m
A. 41
B. 44
C. 42
D. 43
Cho các số thực dương a,b thỏa mãn
log
a
x
,
log
b
y
. Tính
P
log
(
a
2
b
3
)
Đọc tiếp
Cho các số thực dương a,b thỏa mãn log a = x , log b = y . Tính P = log ( a 2 b 3 )
9 tháng 4 2021 lúc 21:22
Cho x,y là các số thực dương thỏa mãn điều kiện x+y-6xy=0 và xy≠1. Tìm giá trị lớn nhất của
M=\(\dfrac{\dfrac{x+1}{xy+1}+\dfrac{xy+x}{1-xy}+1}{1-\dfrac{xy+x}{xy-1}-\dfrac{x+1}{xy+1}}\)
\(6xy=x+y\ge2\sqrt[]{xy}\Rightarrow\sqrt{xy}\ge\dfrac{1}{3}\Rightarrow xy\ge\dfrac{1}{9}\Rightarrow\dfrac{1}{xy}\le9\)
\(M=\dfrac{\dfrac{x+1}{xy+1}+\dfrac{xy+x}{1-xy}+1}{1+\dfrac{xy+x}{1-xy}-\dfrac{x+1}{xy+1}}=\dfrac{\dfrac{x+1}{xy+1}+\dfrac{x+1}{1-xy}}{\dfrac{x+1}{1-xy}-\dfrac{x+1}{xy+1}}=\dfrac{\dfrac{1}{1-xy}+\dfrac{1}{1+xy}}{\dfrac{1}{1-xy}-\dfrac{1}{1+xy}}\)
\(M=\dfrac{1+xy+1-xy}{1+xy-1+xy}=\dfrac{2}{2xy}=\dfrac{1}{xy}\le9\)
Dấu "=" xảy ra khi \(x=y=\dfrac{1}{3}\)
Đúng 1
Bình luận (0)