Cho tam giác cân đỉnh A, ABC với B A C ^ = 120 o , AB=a. Cho △ A B C quay quanh AB tạo thành khối tròn xoay có thể tích V. Tính V.
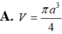
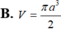
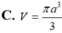
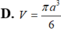
.1.Cho tam giác ABC cân tại A có AD là đường phân giác.
a) Chứng minh tam giác ABD = tam giác ACD
b) Gọi G là trọng tâm tam giác ABC. Chứng minh ba điểm A, G, D thẳng hàng.
c) Tính DG biết AB 13cm,BC 10cm
2.Cho tam giác ABC vuông ở A, có AB = 16cm,AC = 30cm. Tính tổng các khoảng cách từ trọng tâm G của tam giác đến các đỉnh của tam giác.
3.Cho tam giác ABC, trung tuyến AM. Từ M kẻ đường thẳng song song với AB cắt C ở N. Biết AN = MN, BN cắt AM ở O. Chứng minh: a) Tam giác ABC cân ở A
b) O là trọng tâm tam giác ABC.
4.Cho tam giác cân ABC, trung tuyến AM. Đường trung trực của AB cắt AM ở O. Chứng minh rằng điểm O cách đều 3 đỉnh của tam giác ABC.
Cần gấp ạ!
Cho tam giác ABC cân tại A có d là đường trung trực AB vẽ phân giác AE của góc BAC ( E thuộc BC ) d cắt AE tại O a, AE là đường trung trực của tam giác ABC b, O thuộc đường trung trực của đoạn thẳng AC c, O cách đều 3 đỉnh của tam giác ABC
a: ΔABC cân tại A
mà AE là phân giác
nên AE là trung trực của BC
b: O nằm trên trung trực của AB
=>OA=OB
O nằm trên trung trực của BC
=>OB=OC
=>OA=OC
=>O nằm trên trung trực của AC
c: OA=OB=OC
=>O cách đều 3 đỉnh của ΔABC
Cho tam giác ABC góc A bằng 120 độ các tia phân giác của góc A và C cắt nhau ở O, cắt các cạnh BC và AB lần lượt ở D và E. Đường phân giác góc ngoài tại đỉnh B của tam giác ABC cắt đường thẳng AC tại F. Chứng minh a,BO vuông góc với BF b, góc BDF bằng góc ADF c, 3 điểm D, E, F thẳng hàng
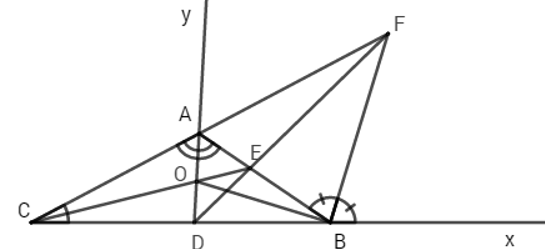
a) Xét \(\Delta ABC\) có tia phân giác \(BAC,ACB\) cắt nhau tại O suy ra O là giao điểm của 3 đường phân giác trong tam giác ABC suy ra BO là phân giác của \(\widehat{CBA}\) (tính chất 3 đường phân giác của tam giác)
\(\Rightarrow DBO=ABO=\dfrac{DBA}{2}\left(1\right)\) ( tính chất tia phân giác )
Lại có BF là phân giác của \(\widehat{ABx\left(gt\right)}\) \(=ABF=FBx\left(2\right)\)
( tính chất của tia phân giác )
Mà \(ABD+ABx=180^o\left(3\right)\left(kềbu\right)\)
Từ \(\left(1\right)\left(2\right)\left(3\right)\Rightarrow OBA+ABF=180^o\div2=90^o\Rightarrow BO\text{⊥ }BF\)
b) Ta có \(FAB+BAC=180^o\)( kề bù ) mà \(BAC=120^o\left(gt\right)\Rightarrow FAB=60^o\)
\(\Rightarrow\text{AD là phân giác của}\widehat{BAC}\) ( dấu hiệu nhận biết tia phân giác )
\(\Rightarrow BAD=CAD=60^o\) ( tính chất tia phân giác )
\(\Rightarrow FAy=CAD=60^o\) ( đối đỉnh ) \(\Rightarrow FAB=FAy=60^o\Rightarrow\) AF là tia phân giác của \(BAy\) ( dấu hiệu nhận biết tia phân giác )
Vậy \(\Delta ABD\) có hai tia phân giác của hai góc ngoài tại đỉnh A và đỉnh B cắt nhau tại F nên suy ra DF là phân giác của \(ADB=BDF=ADF\) ( tính chất tia phân giác )
c) Xét \(\Delta ACD\) có phân giác góc ngoài tại đỉnh A và phân giác trong tại đỉnh C cắt nhau tại E nên suy ra DE cũng là phân giác của \(ADB\Rightarrow\)\(D,E,F\) thẳng hàng
So sánh các cạnh của tam giác ABC biết A) góc ngoài của đỉnh góc A =120° ; góc B = 50° B) tam giác ABC cân tại A ,A>60° C) A=40° và số đo góc B và C tỉ lệ với 3 ; 4
c) Xét ΔABC có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)(Định lí tổng ba góc trong một tam giác)
\(\Leftrightarrow\widehat{B}+\widehat{C}=180^0-40^0=140^0\)
Ta có: \(\widehat{B}:\widehat{C}=3:4\)(gt)
nên \(\dfrac{\widehat{B}}{3}=\dfrac{\widehat{C}}{4}\)
mà \(\widehat{B}+\widehat{C}=140^0\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{\widehat{B}}{3}=\dfrac{\widehat{C}}{4}=\dfrac{\widehat{B}+\widehat{C}}{3+4}=\dfrac{140^0}{7}=20^0\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{\widehat{B}}{3}=20^0\\\dfrac{\widehat{C}}{4}=20^0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\widehat{B}=60^0\\\widehat{C}=80^0\end{matrix}\right.\)
Xét ΔABC có \(\widehat{A}< \widehat{B}< \widehat{C}\left(40^0< 60^0< 80^0\right)\)
mà cạnh đối diện với \(\widehat{A}\) là cạnh BC
cạnh đối diện với \(\widehat{B}\) là cạnh AC
và cạnh đối diện với \(\widehat{C}\) là cạnh AB
nên BC<AC<AB
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(A\), \(\widehat{BAC}=120^o\), \(AB=AC=a\). Tam giác \(SAB\) vuông tại \(B\), tam giác \(SAC\) vuông tại \(C\), góc giữa hai mặt phẳng \(\left(SAB\right)\) và \(\left(ABC\right)\) bằng \(60^o\). Gọi \(H\) là hình chiếu vuông góc của điểm \(S\) lên mặt phẳng \(\left(ABC\right)\). Chứng minh rằng \(HB\) vuông góc \(AB\) và tính thể tích khối chóp \(S.ABC\) theo \(a\)
Cho tam giác ABC cân ở A, M nằm trên AB, N nằm trên AC sao cho BM=AN. Gọi O là điểm cách đều 3 đỉnh A,B,C. Cmr O cách đều M và N ?
cho tam giác ABC cân tại A kẻ AH vuông góc với BC(H thuộc BC)
a, Chứng minh: tam giác AHC= tam giác AHC
b, Kẻ HD vuông góc với AB(D thuộc AB), HE vuông góc với AC(E thuộc AC): Chứng minh tam giác HDE Cân
c,Nếu cho góc A=120 độ thì tam giác HDE trở thành tam giác gì? Vì sao?
1.Cho tam giác ABC các tia phân giác của góc B và góc C cắt nhau ở O..Gọi DEF lần lượt là chân đường vuông góc kẻ từ điểm O đến BC,CA,AB(D thuộc BC,E thuộc AC,F thuộc AB) tia Ao cắt BC ở M.CMR a,OD=OE=OF b,Góc MOC=góc DOB 2.Cho tam giác abc có góc A bằng 120 độ.Các tia phân giác của góc A và góc C cắt nhau ở O,cắt các cạnh BC và AB lần lượt ở D và E.Đường phân giác góc ngoài tại đỉnh B của tam giác ABC cắt đường thẳng AC ở F.CM a,BO vuông góc BF b,góc BDF=góc ADF c,3 điểm DEF thẳng hàng 3.CMR 1 tam giác có 1 trung tuyến đồng thời là phân giác thì tam giác đó là tam giác cân CẦN 1 AI ĐÓ GIẢI HỘ Ạ!!MAI PHẢI NỘP RỒI AI LÀM DÙM VỚI Ạ!!
Cho tam giác ABc cân tại A,có góc A=120.Từ B kẻ vuônng góc với AB,Tù C kẻ vuông góc với AC cắt nhau tại M.Hỏi tam giác MBC là tam giácgì?
Cho Tam giác ABC cân tại A có A = 120 . Trên BC lấy M và N sao cho MA vg góc với AB , NB vg góc AC
a) chứng minh Tam giác BAM = tam giác CAN
b) Tam giác ANB = TAM GIÁC AMC