Cho I = 1 2 ∫ 0 1 x 1 + 2 x d x và u = 2 x + 1 Mệnh đề nào dưới đây sai?
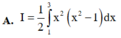
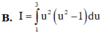
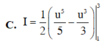
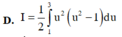
Bài 1 : 1)
Cho biểu thức A = (1/1-x+2/x+1-5-x/1-x^2):1-2x/x^2-1
a) Rút gọn A
b) Tìm x để A>0
Bài 2 :
Cho x, y khác 0 thỏa mãn x^2-2xy+2y^2-2x-2y+5=0 . Tính GTBT P=xy+x+y+13/4xy
Bài 3 : Cho a, b >0 thỏa mãn a+b=1. Tìm GTNN của P=1/ab+40(a^4+b^4)
Bài 1:
a: \(A=\left(\dfrac{1}{1-x}+\dfrac{2}{x+1}-\dfrac{5-x}{1-x^2}\right):\dfrac{1-2x}{x^2-1}\)
\(=\dfrac{-x-1+2x-2-x+5}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{\left(x-1\right)\left(x+1\right)}{1-2x}\)
\(=\dfrac{2}{1-2x}\)
b: Để A>0 thì 1-2x>0
=>2x<1
=>x<1/2
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
Bài 1: Cho x+y+z =0 và x^2+ y^2 + z^2=14
Tính S= x^4+y^4+z^4
Bài 2: Cho 1/x +1/y +1/z= 13 và x+y+z= xyz
Tính S= 1/x^2 +1/y^2 +1/z^2
Bài 3: Cho a,b,c khác 0 và a+b+c = 0
Tính S= 1/ a^2+b^2-c^2 + 1/b^2+c^2-a^2 +1/ c^2+a^2-b^2
Bài 4: Cho x>y>0 và 3x^2+ 3y^2 = 10xy
Tính S= x-y / x+y
Bài 5: Cho a^2+4b+4 và b^2+ 4c+4 và c^2+ 4a+4 = 0
Tính S= a^18+ b^18+ c^18
cho I = Limx→0 2(√3x+1 -1)/x và J = limx→-1 x2-x-2 / x+ 1. tính I-J
X
\(\lim\limits_{x\rightarrow0}\dfrac{2\left(\sqrt{3x+1}-1\right)}{x}=\lim\limits_{x\rightarrow0}\dfrac{6x}{x\left(\sqrt{3x+1}+1\right)}=\lim\limits_{x\rightarrow0}\dfrac{6}{\sqrt{3x+1}+1}=3\)
\(\lim\limits_{x\rightarrow-1}\dfrac{\left(x+1\right)\left(x-2\right)}{x+1}=\lim\limits_{x\rightarrow-1}\left(x-2\right)=-3\)
\(\Rightarrow I-J=6\)
Cho PT:x^2-2(m-1)x+2m-5=0
a)CMR: phương trình luôn có 2 nghiệm phân biệt x1,x2 với mọi m
b)Tìm giá trị m để (x1^2-2mx1+2m-1)(x2^2-2mx2+2m-1) <0
a)PT: \(x^2-2\left(m-1\right)x+2m-5=0\)
\(\Rightarrow\Delta=\left(-2\left(m-1\right)\right)^2-4.1.\left(2m-5\right)\\ =4m^2-16m+24=\left(2m-4\right)^2+8\ge8\left(\forall m\in R\right)\)
Vậy phương trình luôn có hai nghiệm phân biệt \(x_1,x_2\) với mọi m.
p/s: phần (b) mình sẽ giúp bạn trả lời sau nha!
BÀI 1.
CHỨNG MINH:
a) a^2(a+1)+2a(a+1) chia hết cho 6 vs a thuộc Z
b) a(2a-3)-2a(a+1) chia hết cho 5 vs a thuộc Z
BÀI 2.
a) 36x^2-49=0
b(x-1)(x+1)=x+2
c) x^2(x+1)+2x(x+1)=0
d) x(2x-3)-2(3-2x)=0
e) 2x^3(2x-3)-x^2(4x^2-6x+z)=0
f)(x-2)^2-(x+3)^2=5+4(x+1)
a) \(36x^2-49=0\)
\(\Leftrightarrow\left(6x\right)^2-7^2=0\)
\(\Leftrightarrow\left(6x-7\right)\left(6x+7\right)=0\)
\(TH_1:6x-7=0\) \(TH_2:6x+7=0\)
\(\Leftrightarrow6x=7\) \(\Leftrightarrow6x=-7\)
\(\Leftrightarrow x=\dfrac{7}{6}\) \(\Leftrightarrow x=-\dfrac{7}{6}\)
Vậy pt có tập nghiệm \(S=\left\{\dfrac{7}{6};-\dfrac{7}{6}\right\}\)
Bài 2
a) 36x2-49=0
⇔ (6x)2-49=0
⇔(6x-7).(6x+7)=0
TH1: 6x-7=0 TH2: 6x+7=0
⇔6x=7 ⇔6x=-7
⇔x=7/6 ⇔x=-7/6
Bài 1: cho x+y+z=0 và x^2+y^2+z^2=14 .Tính S=x^4+y^4+z^4
Bài 2: cho x>y>0 và a+b+c=0.Tính S= \(\dfrac{1}{a^2+b^2-c^2}\)+\(\dfrac{1}{b^2+c^2-a^2}\)+\(\dfrac{1}{c^2+a^2-b^2}\)
bài 3: cho a^2 +4b +4=0
b^2 +4c+4=0
c^2 +4a+4=0 .Tính S=a^18+b^18+c^18
1,
\(x^2+y^2+y^2=14\)
\(\Rightarrow\left(x+y+z\right)^2-2xy-2yz-2zx=14\)
\(\Rightarrow-2\left(xy+yz+zx\right)=14\)
\(\Rightarrow xy+yz+zx=-7\)
\(\Rightarrow\left(xy+yz+zx\right)^2=49\)
\(\Leftrightarrow x^2y^2+y^2z^2+z^2x^2+2x^2yz+2xy^2z+2xyz^2=49\)
\(\Leftrightarrow x^2y^2+y^2z^2+z^2x^2+2xyz\left(x+y+z\right)=49\)
\(\Leftrightarrow x^2y^2+y^2z^2+z^2x^2=49\)
Ta có: \(x^4+y^4+z^4\)
\(=\left(x^2+y^2+z^2\right)^2-2x^2y^2-2y^2z^2-2z^2x^2\)
\(=14^2-2\left(x^2y^2+y^2z^2+z^2x^2\right)\)
\(=14^2-2.49\)
\(=196-98\)
\(=98\)
Cho : A =( \(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{1}{x-\sqrt{x}}\)) +\(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{x-1}\)(x < 0 ; x ≠ 1 )
a, Rút gọn
b, 1; tim x 2; c/m A < 0
a: \(A=\dfrac{x+1}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{x-1}\)
\(=\dfrac{\left(x+1\right)\left(\sqrt{x}+1\right)+\sqrt{x}\left(\sqrt{x}-1\right)+2\sqrt{x}}{\sqrt{x}\left(x-1\right)}\)
\(=\dfrac{x\sqrt{x}+x+\sqrt{x}+1+x-\sqrt{x}+2\sqrt{x}}{\sqrt{x}\left(x-1\right)}\)
\(=\dfrac{x\sqrt{x}+2x+2\sqrt{x}+1}{\sqrt{x}\left(x-1\right)}\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)+2\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}\left(x-1\right)}\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
b: Để A<0 thì \(\sqrt{x}-1< 0\)
=>0<x<1
Giải phương trình:
1. (x - 4)2 - 25 = 0
2. (x - 3)2 - (x - 1)2 = 0
3. (x2 - 4)(2x +3) = (x2 - 4)(x - 1)
4. (x2 - 1) - (x + 1)(2 - 3x) = 0
5. x3 + x2 + x + 1 = 0
6. x3 + x2 - x - 1 = 0
7. 2x3 + 3x2 + 6x + 5 = 0
8. x4 - 4x3 - 19x2 + 106x - 120 = 0
9. (x2 - 3x + 2)(x2 + 15x + 56) + 8 = 0
1 ) \(\left(x-4\right)^2-25=0\)
\(\Leftrightarrow\left(x-4-5\right)\left(x-4+5\right)=0\)
\(\Leftrightarrow\left(x-9\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=9\\x=-1\end{matrix}\right.\)
2 ) \(\left(x-3\right)^2-\left(x-1\right)^2=0\)
\(\Leftrightarrow\left(x-3+x-1\right)\left(x-3-x+1\right)=0\)
\(\Leftrightarrow-2\left(2x-4\right)=0\)
\(\Leftrightarrow x=2.\)
3 ) \(\left(x^2-4\right)\left(2x+3\right)=\left(x^2-4\right)\left(x-1\right)\)
\(\Leftrightarrow\left(x^2-4\right)\left(2x+3-x+1\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\\x=-4\end{matrix}\right.\)
4 ) \(\left(x^2-1\right)-\left(x+1\right)\left(2-3x\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-1-2+3x\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(4x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{3}{4}\end{matrix}\right.\)
5 ) \(x^3+x^2+x+1=0\)
\(\Leftrightarrow\left(x^2+1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2=-1\left(loại\right)\\x=-1.\end{matrix}\right.\)
6 ) \(x^3+x^2-x-1=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
7 ) \(2x^3+3x^2+6x+5=0\)
\(\Leftrightarrow2x^3+2x^2+x^2+x+5x+5=0\)
\(\Leftrightarrow2x^2\left(x+1\right)+x\left(x+1\right)+5\left(x+1\right)=0\)
\(\Leftrightarrow\left(2x^2+x+5\right)\left(x+1\right)=0\)
\(\Leftrightarrow x=-1.\)
8 ) \(x^4-4x^3-19x^2+106x-120=0\)
\(\Leftrightarrow x^4-4x^3-19x^2+76x+30x-120=0\)
\(\Leftrightarrow x^3\left(x-4\right)-19x\left(x-4\right)+30\left(x-4\right)=0\)
\(\Leftrightarrow\left(x^3-19x+30\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left(x^3-8-19x+38\right)\left(x-4\right)\)
\(\Leftrightarrow\left(x-2\right)\left(x^2+4x+23\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=4\end{matrix}\right.\)
9 ) \(\left(x^2-3x+2\right)\left(x^2+15x+56\right)+8=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-1\right)\left(x+7\right)\left(x+8\right)+8=0\)
\(\Leftrightarrow\left(x^2+7x-x-7\right)\left(x^2+8x-2x-16\right)+8=0\)
\(\Leftrightarrow\left(x^2+6x-7\right)\left(x^2+6x-16\right)+8=0\)
Đặt \(x^2+6x-7=t\)
\(\Leftrightarrow t\left(t-9\right)+8=0\)
\(\Leftrightarrow t^2-9t+8=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=8\\t=1\end{matrix}\right.\)
Khi t = 8 \(\Leftrightarrow x^2+6x-7=8\Leftrightarrow x^2+6x-15\Leftrightarrow\left[{}\begin{matrix}x=-3+2\sqrt{6}\\x=-3-2\sqrt{6}\end{matrix}\right.\)
Khi t = 1 \(\Leftrightarrow x^2+6x-7=1\Leftrightarrow x^2+6x-8=0\Leftrightarrow\left[{}\begin{matrix}x=-3+\sqrt{17}\\x=-3-\sqrt{17}\end{matrix}\right.\)
Vậy ........
Bài 1: Giải các pt sau: 1) x2 + 5x + 6 = 0 2)
x2 - x - 6 = 0
3) (x2 + 1) (x2 + 4x + 4) = 0
4) x3 + x2 + x + 1 = 0
5) x2 - 7x + 6 = 0
6) 2x2 - 3x - 5 = 0
7) x2 + x - 12 = 0
8) 2x3 + 6x2 = x2 + 3x
9) (3x - 1) (x2 + 2) = (3x - 1)(7x - 10)
Bài 2: Cho biểu thức A = (5x - 3y + 1) (7x + 2y -2) a) Tìm x sao cho với y = 2 thì A = 0 b) Tìm y sao cho với x = -2 thì A = 0