Tập xác định của hàm số f x = log - x 2 - 2 x + 8 x + 1 có chứa bao nhiêu số nguyên
A. 4
B. 7
C. 3
D. 5
Tập xác định của hàm số f ( x ) = log - x 2 - 2 x + 8 | x + 1 | có chứa bao nhiêu số nguyên?
A. 4
B. 7
C. 3
D. 5
Chọn A
Điều kiện:

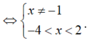
Vậy tập xác định của hàm số f(x) là ![]() suy ra tập xác định của hàm số chứa 4 số nguyên là -3; -2; 0; 1
suy ra tập xác định của hàm số chứa 4 số nguyên là -3; -2; 0; 1
Tập xác định của hàm số f ( x ) = log - x 2 - 2 x + 8 x + 1 có chứa bao nhiêu số nguyên?
A. 4
B. 7
C. 3
D. 5
Tìm tập xác định của hàm số log ( x 2 - x - 2 )
![]()
![]()
![]()
![]()
Tìm tập xác định của hàm số y = log x 2 - x - 2
A. - ∞ ; 2
B. 1 ; + ∞
C. - ∞ ; - 1 ∪ 2 ; + ∞
D. - 1 ; 1
Tìm tập xác định của hàm số y = log ( x 2 - x - 2 )
A. ( - ∞ ; - 1 ) ∪ ( 2 ; + ∞ )
B. ( - ∞ ; 2 )
C. ( 1 ; + ∞ )
D. (-1; 1)
Tìm tập xác định của hàm số y=log ( x2-x-2)
![]()
![]()
![]()
![]()
Tìm tập xác định của hàm số y = log ( x 2 - x - 2 ) ( 1 )
A . ( - ∞ ; 1 ) ∪ ( 2 ; + ∞ )
B . ( - ∞ ; 2 )
C . ( 1 ; + ∞ )
D . ( - 1 ; 1 )
Chọn A
Điều kiện xác định:

Vậy tập xác định của hàm số (1) là ![]()
Tìm tập xác định D của hàm số y = l o g ( x 2 - x - 2 ) (1)
![]()
![]()
![]()
![]()
Tìm tập xác định của các hàm số:
a) \({\log _2}\left( {3 - 2{\rm{x}}} \right)\);
b) \({\log _3}\left( {{x^2} + 4{\rm{x}}} \right)\).
a) \(log_2\left(3-2x\right)\) xác định khi \(3-2x>0\) hay \(x< \dfrac{3}{2}\)
b) \(log_3\left(x^2+4x\right)\) xác định khi \(x^2+4x>0\) hay \(x>0\) hoặc \(x< -4\)
Tìm tập xác định của các hàm số sau:
a) \(y = \log \left| {x + 3} \right|;\)
b) \(y = \ln \left( {4 - {x^2}} \right).\)
a, \(y=log\left|x+3\right|\) có nghĩa khi \(\left|x+3\right|>0\)
Mà \(\left|x+3\right|\ge0\forall x\in R\)
\(\Rightarrow\) \(\left|x+3\right|>0\) khi \(x\ne-3\)
Vậy tập xác định của hàm số là D = R \ {-3}.
b, \(y=ln\left(4-x^2\right)\) có nghĩa khi \(4-x^2>0\)
\(\Rightarrow x^2< 4\\ \Leftrightarrow-2< x< 2\)
Vậy tập xác định của hàm số là D = (-2;2).