Cho lăng trụ đứng ABCA'B'C' có đáy ABC là tam giác vuông tại A, AB=a, A C B ^ = 60 ° , B'C tạo với mặt phẳng AA'CC' một góc 30 ° . Thể tích của khối lăng trụ ABCA'B'C' bằng
![]()
![]()
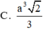
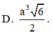
Cho lăng trụ đứng A B C A ' B ' C ' có đáy ABC là tam giác vuông tại A, A B = a , A C B = 60 ° , B ' C tạo với mặt phẳng AA'CC' một góc 30 ° . Tính thể tích V của khối lăng trụ A B C A ' B ' C ' .
A. V = a 3 2
B. V = a 3 3
C. V = a 3 2 3
D. V = a 3 6 2
Cho hình lăng trụ đứng ABCA'B'C' có đáy ABC là tam giác vuông cân tại A, mặt bên BCC'B' là hình vuông cạnh 2 α . Thể tích của khối lăng trụ ABCA'B'C' bằng
![]()
![]()

![]()
Cho lăng trụ đứng A B C A ' B ' C ' có đáy ABC là tam giác vuông tại A, A B = a , A C B = 60 ° , B'C tạo với mặt phẳng A A ' C C ' một góc 30 ° . Thể tích của khối lăng trụ bằng
A. a 3 2
B. a 3 3
C. a 3 2 3
D. a 3 6 2
Chọn C.
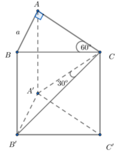
Phương pháp: Sử dụng định ly Pytago và lượng giác để tính các cạnh.

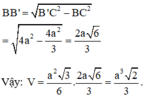
cho hình lăng trụ đứng ABCA'B'C' có đáy tam giác ABC vuông cân tại A, BC=a, góc giữa BC' và đáy 45°. tính thể tích ABCA'B'C'
Cho lăng trụ ABCA'B'C' có đáy ABC là tam giác vuông tại B, AB=a, BC=2a. Biết lăng trụ có thể tích V = 2 a 3 tính khoảng cách d giữa hai đáy của lăng trụ theo a.
A. d = 3 a .
B. d = a .
C. d = 6 a .
D. d = 2 a .
Đáp án D
S A B C = 1 2 a .2 a = a 2 ⇒ d = V S = 2 a 3 a 2 = 2 a
Cho hình lăng trụ đứng ABCA'B'C' có đáy ABC là tam giác vuông cân tại A, mặt bên BCC'B' là hình vuông cạnh 2a. Tính thể tích V của khối lăng trụ
A. V = a 3
B. V = a 3 2
C. V = 2 a 3 3
D. V = 2 a 3
Cho lăng trụ đứng =ABCA'B'C' có đáy ABC là tam giác cân tại A, A B = a 2 , A ' A = a .Thể tích V của khối chóp A.A'ACC' là.
A. V = 2 a 3
B. V = 3 a 3
C. V = 2 a 3 3
D. V = a 3
cho hình lăng trụ đứng ABCA'B'C' có đáy là tam giác cân tại A, AB=a, góc BAC=120°. góc giữa (A'BC) và (ABC)=60°. tính VABCA'B'C'
Cho lăng trụ đứng ABCA'B'C' có đáy là tam giác vuông cân tại A với AB = AC = a, A'B tạo với đáy 1 góc α biết tanα = 2
a, Tính (A'B; (BCC'B'))
b, Tính (C'B; (A'B'BA))
\(A'A\perp\left(ABC\right)\) theo giả thiết \(\Rightarrow\widehat{A'BA}\) là góc giữa A'B và đáy
\(\Rightarrow tan\widehat{A'BA}=2\Rightarrow A'A=AB.tan\widehat{A'BA}=2a\)
a.
Gọi D' là trung điểm B'C' \(\Rightarrow A'D'\perp B'C'\) (đáy là tam giác vuông cân)
\(\Rightarrow A'D'\perp\left(BCC'B'\right)\Rightarrow\widehat{A'BD'}\) là góc giữa A'B và (BCC'B')
\(A'B=\sqrt{AB^2+A'A^2}=a\sqrt{5}\)
\(A'D'=\dfrac{1}{2}B'C'=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow sin\widehat{A'BD'}=\dfrac{A'D'}{A'B}=\dfrac{\sqrt{10}}{10}\Rightarrow\widehat{A'BD'}\approx18^026'\)
b.
\(\left\{{}\begin{matrix}A'C'\perp A'B'\left(gt\right)\\A'A\perp\left(A'B'C'\right)\Rightarrow A'A\perp A'C'\end{matrix}\right.\)
\(\Rightarrow A'C'\perp\left(ABB'A'\right)\Rightarrow\widehat{C'BA'}\) là góc giữa C'B và (ABB'A')
\(tan\widehat{C'BA'}=\dfrac{A'C'}{A'B}=\dfrac{a}{a\sqrt{5}}=\dfrac{1}{\sqrt{5}}\)
\(\Rightarrow\widehat{C'BA'}\approx24^06'\)