Trong không gian Oxyz, cho tam giác ABC với A (3;0;0), B (0;6;0), C (0;0;6). Phương trình nào dưới đây là phương trình đường thẳng đi qua trực tâm của tam giác ABC và vuông góc với mặt phẳng (ABC).
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(0;1;4), B(3;-1;1), C(-2;3;2). Tính diện tích tam giác ABC.
A. S = 2 62 .
B. S = 12.
C. S = 6 .
D. S = 62 .
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(0;1;4), B(3;-1;1), C(-2;3;2). Tính diện tích tam giác ABC
A. S = 2 62
B. S = 12
C. S = 6
D. S = 62
Trong không gian Oxyz, cho tam giác ABC với A(1;2;3),B(-10;-5;-1),C(-3;-9;10). Phương trình đường phân giác kẻ từ đỉnh A của tam giác ABC là
A. x - 1 3 = y - 2 - 2 = z - 3 3
B. x - 1 - 3 = y - 2 - 2 = z - 3 7
C. x - 1 1 = y - 2 - 1 = z - 3 - 1
D. x - 1 - 5 = y - 2 - 6 = z - 3 1
Trong không gian Oxyz, cho tam giác ABC với A(8;9;2), B(3;5;1), C(11;10;4). Số đo góc A của tam giác ABC là
A. 150 o
B. 60 o
C. 120 o
D. 30 o
Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC có A(0;1;4); B(3;-1;1); C(-2;3;2) Tính diện tích S của tam giác ABC.
A. S = 2 62 .
B. S = 12
C. S = 6 .
D. S = 62 .
Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC có A(0;1;4), B(3;-1;1),C(-2;3;2). Tính diện tích S của tam giác ABC.
A. S = 2 62
B. S =12
C. S = 6
D. S = 62
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(1;1;2), B(-2;3;1), C(3;-1;4). Viết phương trình đường cao của tam giác ABC kẻ từ đỉnh B
A. x = - 2 - t y = 3 + t z = 1 - t
B. x = - 2 + t y = 3 z = 1 - t
C. x = 1 + 2 t y = 3 + t z = 1 + t
D. x = - 2 + t y = 3 - t z = 1 + t
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(1;0;0), B(0;0;1), C(2;1;1). Diện tích tam giác ABC bằng
A. 11 2
B. 7 2
C. 6 2
D. 5 2
Trong không gian Oxyz, cho tam giác ABC với A ( 1 ; - 2 ; 3 ) , B ( - 4 ; 0 ; - 1 ) và C ( 1 ; 1 ; - 3 ) . Phương mặt phẳng (P) đi qua A, trọng tâm G của tam giác ABC và vuông góc với mặt phẳng (ABC) là:
![]()
![]()
![]()
![]()
Đáp án A.
(P) đi qua A và G nên (P) đi qua trung điểm của BC là điểm 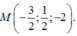
Ta có: 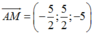 cùng phương với véc tơ (-1;1;-2)
cùng phương với véc tơ (-1;1;-2)
Mặt phằng (ABC) có vác tơ pháp tuyến:
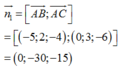
cùng phương với véc tơ (0;2;1)
Vì (P) chứa AM và vuông góc với (ABC) nên (P) có véc tơ chỉ phương:
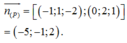
Ngoài ra (P) qua A ( 1 ; - 2 ; 3 ) nên phương trình (P):
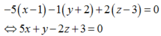
Trong không gian Oxyz, cho tam giác ABC với A 1 ; − 2 ; 3 , B − 4 ; 0 ; − 1 và C 1 ; 1 ; − 3 . Phương mặt phẳng (P) đi qua A, trọng tâm G của tam giác ABC và vuông góc với mặt phẳng (ABC) là
A. 5 x + y − 2 z + 3 = 0.
B. 2 y + z − 7 = 0.
C. 5 x + y − 2 z − 1 = 0.
D. 2 y + z + 1 = 0
Đáp án A.
(P) đi qua A và G nên (P) đi qua trung điểm của BC là điểm
M − 3 2 ; 1 2 ; − 2 .
Ta có: A M → = − 5 2 ; 5 2 ; − 5 cùng phương với véc tơ − 1 ; 1 ; − 2
Mặt phằng (ABC) có vác tơ pháp tuyến:
n 1 → = A B → ; A C → = − 5 ; 2 ; − 4 ; 0 ; 3 ; − 6 = 0 ; − 30 ; − 15
cùng phương với véc tơ 0 ; 2 ; 1 .
Vì (P) chứa AM và vuông góc với (ABC) nên (P) có véc tơ chỉ phương:
n ( P ) → = − 1 ; 1 ; − 2 ; 0 ; 2 ; 1 = − 5 ; − 1 ; 2 .
Ngoài ra (P) qua A 1 ; − 2 ; 3 nên phương trình (P):
− 5 x − 1 − 1 y + 2 + 2 z − 3 = 0 ⇔ 5 x + y − 2 z + 3 = 0