Cho hình chóp S.ABCD có đáy là hình thoi cạnh 2a, góc B A D ^ = 60 o , SAB là tam giác đều nằm trên mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng (SCD) là
A. a 3 2
B. 3 a 2
C. a 6 2
D. a 6
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, A B C ^ = 60 ° . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính diện tích của mặt cầu ngoại tiếp hình chóp S.ABCD.
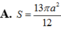
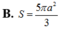
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh 2a, A C = a 3 , SAB là tam giác đều, S A D ^ = 120 ° . Tính thể tích của khối chóp S.ABCD
A. a 3 3
B. 3 a 3 3 2
C. a 3 6
D. 2 a 3 3 3
HD: Gọi H là tâm đường tròn ngoại tiếp ∆SBD

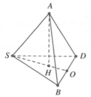
Bán kính đường tròn ngoại tiếp ∆SBD là

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, A B C ^ = 60 ∘ .Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính diện tích S m c của mặt cầu ngoại tiếp hình chóp S.ABC.
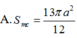
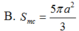
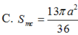
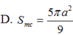
Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, A B C ^ = 60 ° , mặt bên SAB là tam giác đều nằm trong mặt phẳng vuông góc với đáy. Khoảng cách từ điểm A đến mặt phẳng (SCD) bằng
A. a 6 4
B. a
C. a 3 2
D. a 21 7
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, tam giác SAB là tam giác đều nằm trong mặt phẳng tạo với đáy một góc 60 độ. Tính thể tích khối chóp S.ABCD.
A. a 3 4
B. 3 a 3 4
C. a 3 3 6
D. a 3 3 4
Cho hỉnh chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Mặt bên SAB là tam giác đều và vuông góc với đáy. Thể tích khối cầu ngoại tiếp hình chóp S.ABCD là
A. V = 28 πa 3 7 9
B. V = 28 πa 3 21 27
C. V = 4 πa 3 21 27
D. V = 16 πa 3 3 27
Cho hình chóp S . A B C D có đáy A B C D là hình thang vuông tại A và D, S A B là tam giác đều cạnh 2 a và mặt phẳng S A B vuông góc với mặt phẳng A B C D . Tính cosin của góc giữa hai mặt phẳng S A B và S B C
A. 2 7
B. 2 6
C. 3 7
D. 5 7
Đáp án là A
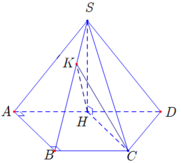
Gọi H là trung điểm của A B . Gọi K là hình chiếu vuông góc của H lên S B .
Khi đó, C K H ^ là góc giữa hai mp
Ta có: S H = 2 a 3 2 = a 3 ; S B = 2 a ; H B = a ⇒ H K = a 3 2 ; C K = a 7 2 .
Vậy cos C K H ^ = 3 7
Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, góc = 450, tam giác SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Thể tích của hình chóp S.ABCD là:
A. a 3 2
B. a 3 6
C. a 3 2 2
D. a 3 2 12
Cho hình chóp S.ABCD có đá ABCD là hình thoi cạnh 2 a , A C = 3 a , S A B là tam giác đều, S A D ^ = 120 ° . Tính thể tích khối chóp S.ABCD
A. 3 a 3
B. 3 3 a 3 2
C. 6 a 3
D. 2 3 a 3 3