HD: Gọi H là tâm đường tròn ngoại tiếp ∆SBD

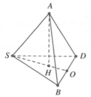
Bán kính đường tròn ngoại tiếp ∆SBD là

HD: Gọi H là tâm đường tròn ngoại tiếp ∆SBD


Bán kính đường tròn ngoại tiếp ∆SBD là

Cho hình chóp S.ABCD có đá ABCD là hình thoi cạnh 2 a , A C = 3 a , S A B là tam giác đều, S A D ^ = 120 ° . Tính thể tích khối chóp S.ABCD
A. 3 a 3
B. 3 3 a 3 2
C. 6 a 3
D. 2 3 a 3 3
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy, SA = 2a . Tính theo a thể tích khối chóp S.ABCD.
A. V = a 3 15 12
B. V = a 3 15 6
C. V = 2 a 3 3
D. V = 2 a 3
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy, SA=2a. Thể tích khối chóp S.ABCD theo a là:
A. a 3 15 6
B. a 3 15 12
C. 2 a 3 3
D. 2 a 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy và SA=a 3 . Tính thể tích V của khối chóp S.ABCD
A. V= 3 a 3
B. V= 3 3 a 3
C. V= a 3
D. V=1/3 a 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích V của khối chóp S.ABCD.
A. V = a 3 3 12 .
B. V = a 3 3 6 .
C. V = a 3 3 4 .
D. V = a 3 3 9 .
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB là tam giác đều nằm trong mặt phẳng tạo với đáy một góc 600. Tính thể tích khối chóp S.ABCD
A. a 3 4
B. 3 a 3 4
C. a 3 3 6
D. a 3 3 4
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB=BC=2, AD=3. Cạnh bên SA=2 và vuông góc với đáy. Tính thể tích khối chóp S.ABCD.
A. V = 4
B. V = 10 3
C. V = 10 3 3
D. V = 17 6
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp S. ABCD bằng
A. 3 6 a 3
B. 3 3 a 3
C. 1 3 a 3
D. 2 3 a 3
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều, S C = S D = a 3 . Tính thể tích V của khối chóp S.ABCD theo a.
A. V = a 3 2 6 .
B. V = a 3 6 .
C. V = a 3 2 .