Cho số phức z=1+i. Số phức nghịch đảo của z là
A. 1 - i 2
B. 1-i
C. 1 - i 2
D. - 1 + i 2
Cho số phức z = 1+i. Số phức nghịch đảo của z là:
A. 1 - i 2
B. 1 - i
C. 1 - i 2
D. - 1 + i 2
Đáp án C
Phương pháp giải: Ta có
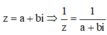
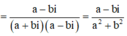
Lời giải: Ta có
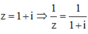
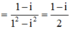
Cho số phức z = 1 + i Số phức nghịch đảo của z là:
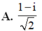
![]()
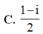
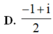
Mô đun số phức nghịch đảo của số phức z = ( 1 - i ) 2 bằng
![]()
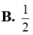
![]()
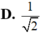
Mô đun số phức nghịch đảo của số phức z = ( 1 - i ) 2 bằng
A. 2
B. 1 2
C. 5
D. 1 2
Cho số phức z = − 1 + 3 i . Số phức nghịch đảo của z có phần ảo là
A. 3 4 i .
B. 3 4 .
C. - 3 4 i .
D. - 3 4 .
Đáp án D
1 z = 1 − 1 + 3 i = − 1 4 − 3 4 i .
Tìm nghịch đảo của số phức z, biết z thỏa mãn | z - 2i| =| z ¯ + 2 + 4i| và z - i z ¯ + i là số thuần ảo.
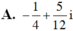
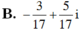

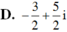
Chọn D.
Giả sử z = a+ bi thì ![]() khi và chỉ khi a = b - 4 (1)
khi và chỉ khi a = b - 4 (1)
Với a ≠ 0 hoặc b ≠ 1, ta có:
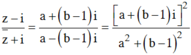
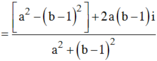
Vì ![]() là số thuần ảo nên a2 - ( b - 1) 2 = 0 khi và chỉ khi a = b - 1 hoặc a = 1 - b
là số thuần ảo nên a2 - ( b - 1) 2 = 0 khi và chỉ khi a = b - 1 hoặc a = 1 - b
Kết hợp (1) ta có a = -3/2 và b = 5/2.
Vậy số phức đó là 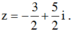
Câu 1 : Cho số phức \(z\) thỏa mãn \(z\) + ( 2 - i )\(\overline{z}\) = 3 - 5i. Môđun của số phức w = \(z \) - i bằng bao nhiêu ?
Câu 2 : Cho số phức \(z\) = a + bi, (a,b ∈ R ) thỏa mãn ( 3 + 2i )\(z\) + ( 2 - i )2 = 4 + i. Tính P = a - b
Cho số phức z = 1+ ( 1+ i) + ( 1+i) 2+ ...+ (1+ i) 26 . Phần thực của số phức z là
A. 2 13
B. - 1 + 2 13
C. - 2 13
D. 1 + 2 13
Chọn A. Số phức z là tổng của cấp số nhân với số hạng đầu là 1 và công bội q = 1 + i. Do đó:
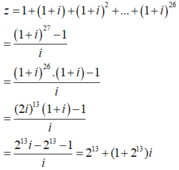
Vậy phần thực là: 213
Tính môđun số phức nghịch đảo của số phức z = ( 1 - 2 i ) 2
A. 1 5
B. 5
C. 1 25
D 1 5