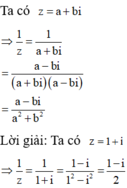Các câu hỏi tương tự
Cho số phức z = 1 + i Số phức nghịch đảo của z là:
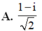
![]()
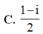
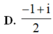
Mô đun số phức nghịch đảo của số phức
z
(
1
-
i
)
2
bằng
Đọc tiếp
Mô đun số phức nghịch đảo của số phức z = ( 1 - i ) 2 bằng
![]()
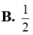
![]()
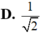
Cho số phức z 1+ ( 1+ i) + ( 1+i) 2+ ...+ (1+ i) 26 . Phần thực của số phức z là A.
2
13
B.
-
1
+
2
13
C.
-
2
13
D.
1
+
2
13
Đọc tiếp
Cho số phức z = 1+ ( 1+ i) + ( 1+i) 2+ ...+ (1+ i) 26 . Phần thực của số phức z là
A. 2 13
B. - 1 + 2 13
C. - 2 13
D. 1 + 2 13
Cho số phức z, biết
(
2
z
-
1
)
(
1
+
i
)
+
(
z
¯
+
1
)
(...
Đọc tiếp
Cho số phức z, biết ( 2 z - 1 ) ( 1 + i ) + ( z ¯ + 1 ) ( 1 - i ) = 2 - 2 i .
Tìm số phức liên hợp của số phức w=3z-3i
A. 1 3 - 1 3 i
B. 1 3 + 1 3 i
C. 1 - 4 i
D. 1 + 4 i
Trong mặt phẳng phức cho các điểm A, B, C theo thứ tự biểu diễn các số phức
z
1
-
i
;
z
2
2
+
i
;
z
3
-
1
+
i
. Tìm số phức z biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành
Đọc tiếp
Trong mặt phẳng phức cho các điểm A, B, C theo thứ tự biểu diễn các số phức z 1 = - i ; z 2 = 2 + i ; z 3 = - 1 + i . Tìm số phức z biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành
![]()
![]()
![]()
![]()
Trong mặt phẳng phức cho các điểm A, B, C theo thứ tự biểu diễn các số phức
z
1
-
i
,
z
2
2
+
i
,
z
3
-
1
+
i
. Tìm số phức z biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành A. z -3 - i B. z -2 – i C. z -1 –...
Đọc tiếp
Trong mặt phẳng phức cho các điểm A, B, C theo thứ tự biểu diễn các số phức z 1 = - i , z 2 = 2 + i , z 3 = - 1 + i . Tìm số phức z biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành
A. z = -3 - i
B. z = -2 – i
C. z = -1 – 3i
D. z = -3
Tìm nghịch đảo của số phức z, biết z thỏa mãn | z - 2i| |
z
¯
+ 2 + 4i| và
z
-
i
z
¯
+
i
là số thuần ảo.
Đọc tiếp
Tìm nghịch đảo của số phức z, biết z thỏa mãn | z - 2i| =| z ¯ + 2 + 4i| và z - i z ¯ + i là số thuần ảo.
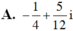
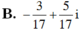

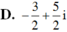
Tìm nghịch đảo của số phức sau:
a) 2 − i 3 ;
b) i;
c) 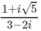 ;
;
d) (3 + i 2 )2.
Cho số phức thỏa mãn
z
-
i
z
-
1
+
2
i
. Tập hợp điểm biểu diễn số phức w (2 - i) z +1 trên mặt phẳng phức là một đường thẳng. Phương trình của đường thẳng đó là
Đọc tiếp
Cho số phức thỏa mãn z - i = z - 1 + 2 i . Tập hợp điểm biểu diễn số phức w = (2 - i) z +1 trên mặt phẳng phức là một đường thẳng. Phương trình của đường thẳng đó là
![]()
![]()
![]()
![]()