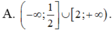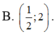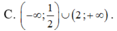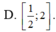Tìm tập xác định của hàm số y = ln ( 1 - x )
A. D = ( - ∞ ; - 1 )
B. D = ( - 1 ; + ∞ )
C. D = ( - ∞ ; 1 )
D. D = ( 1 ; + ∞ )
Tìm tập xác định D của hàm số y = ln ( x - 1 )
![]()
![]()
![]()
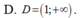
Tìm tập xác định D của hàm số y = l n ( 1 - x ) 2
![]()
![]()
![]()
![]()
Tìm tập xác định của các hàm số sau:
a) \(y = \sqrt {{4^x} - {2^{x + 1}}} \)
b) \(y = \ln (1 - \ln x)\).
\(a,4^x-2^{x+1}\ge0\\ \Leftrightarrow2^{x+1}\le2^{2x}\\ \Leftrightarrow x+1\le2x\\ \Leftrightarrow x\ge1\)
Tập xác định của hàm số là D = \([1;+\infty)\)
\(b,\left\{{}\begin{matrix}x>0\\1-ln\left(x\right)>0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x>0\\ln\left(x\right)< 1\end{matrix}\right.\\ \Leftrightarrow0< x< e\)
Tập xác định của hàm số là \(\left(0;e\right)\)
Tìm tập xác định của hàm số y = ln(1-x).
A . D = ( - ∞ ; - 1 )
B . D = ( 1 ; + ∞ )
C . D = ( - ∞ ; 1 )
D . D = ( 1 ; + ∞ )
Chọn C
Điều kiện xác định: ![]()
Tập xác định của hàm số đã cho là D = ( - ∞ ; 1 )
Tìm tập xác định của hàm số y = ln ( 1 - x ) 2 .
A . ( 1 ; + ∞ )
B . ( - ∞ ; 1 )
C . ℝ
D . ℝ \ { 1 }
Tìm tập xác định của hàm số y = ln ( 1 - x ) 2
A. ( 1 ; + ∞ )
B. ( - ∞ ; 1 )
C. R
D. R \ {1}
Tìm tập xác định của hàm số y = ln ( 1 - x + 1 ) là
A . [ - 1 ; 0 ]
B . ( - 1 ; + ∞ )
C . ( - 1 ; 0 )
D . ( - 1 ; 0 )
Tìm tập xác định D của hàm số y = ln ( x 2 - 3 x )
A. D = (0;3)
B. D = [0;3]
C. D = (-∞;0)∪(3;+∞)
D. D = (-∞;0)∪[3;+∞)
Đáp án C
Phương pháp:
Hàm số y = logaf(x) (0 < a ≠ 1) xác định khi và chỉ khi ⇔ f(x) > 0
Cách giải:
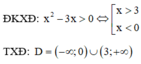
Tìm tập xác định D của hàm số y = l n ( 2 x 2 - 5 x + 2 )