Trong hình bên AH là đường cao của mấy hình tam giác

A. 2
B. 4
C. 6
D. 8
1.Chu vi của hình tròn có đường kính 6dm là:....................dm
2.Trong hình bên,AH là đường cao của mấy hình tam giác ?.
A.3 hình
B.4 hình
C.5 hình
D.6 hình
Câu 1 : 18, 84 dm
Câu 2 ( ko có hình )
Câu 1: `P=6×3,14=18,84(dm)`
2.Trong hình bên,AH là đường cao của mấy hình tam giác ?.
A.3 hình
B.4 hình
C.5 hình
D.6 hình
1.Trong hình bên,AH là đường cao của mấy hình tam giác?
A.3 hình
B.4 hình
C.5 hình D.6 hình
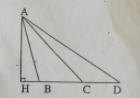 Giúp mk nhé!
Giúp mk nhé!
Trong hình bên AH là đường cao của mấy hình tam giác
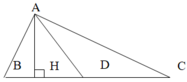
A. 2
B. 4
C. 6
D. 8
đề bài: tam giác ABC có đường cao AH. Điểm M nằm trên cạnh BC a) AH là đường cao của những tam giác nào? b) trong hình bên, tam giác nào có 1 góc tù, tam giác nào có 1 góc vuông?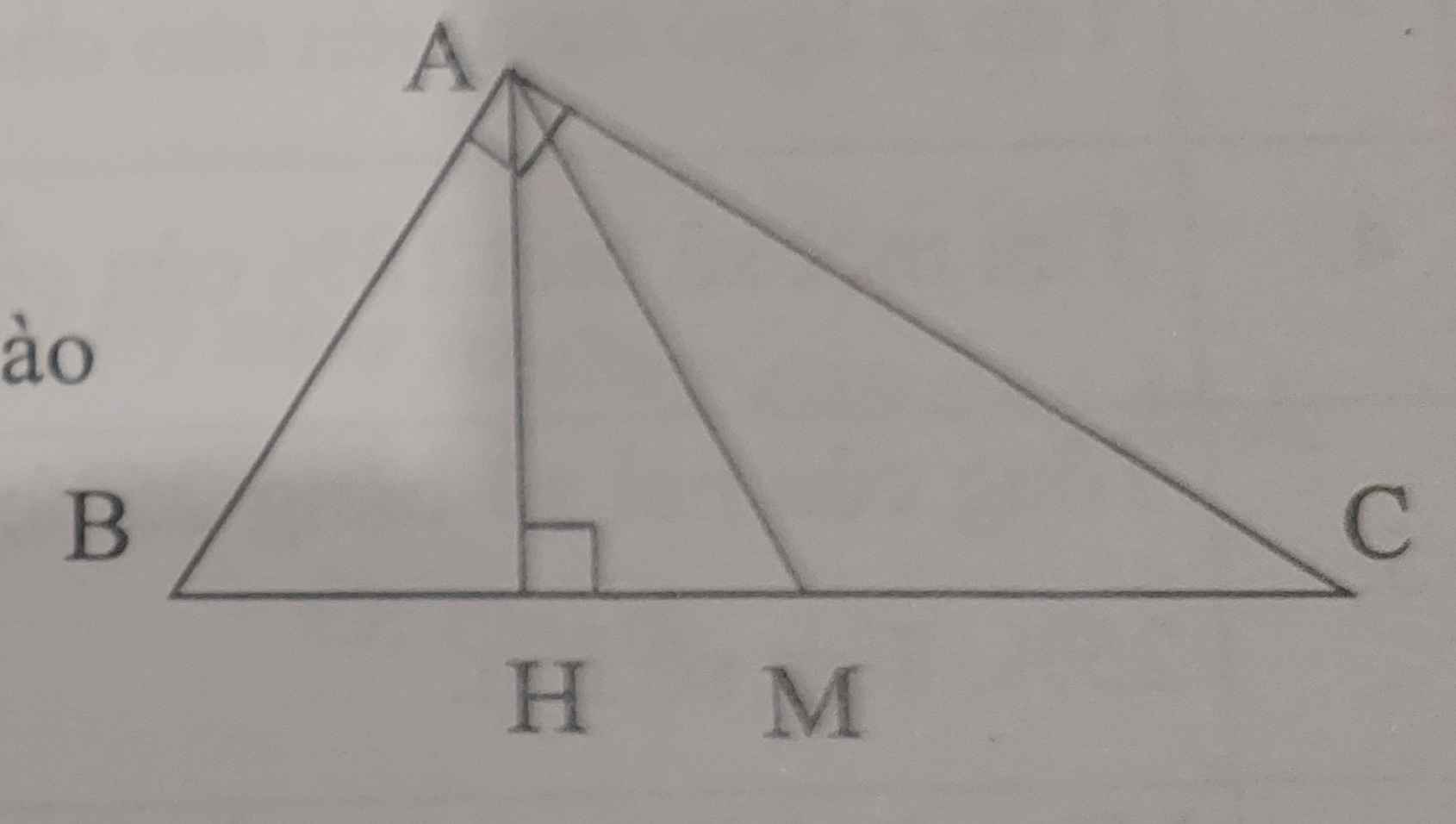
a, \(AH\) là đường cao của \(\Delta ABC,ABM,AHC,AHM,AHB\)
b, \(\Delta AMC\) có 1 góc tù
\(\Delta AHB;\Delta AHC;\Delta AHM\) có 1 góc vuông
đề bài: tam giác ABC có đường cao AH. Điểm M nằm trên cạnh BC
a) AH là đường cao của những tam giác nào?
b) trong hình bên, tam giác nào có 1 góc tù, tam giác nào có 1 góc vuông?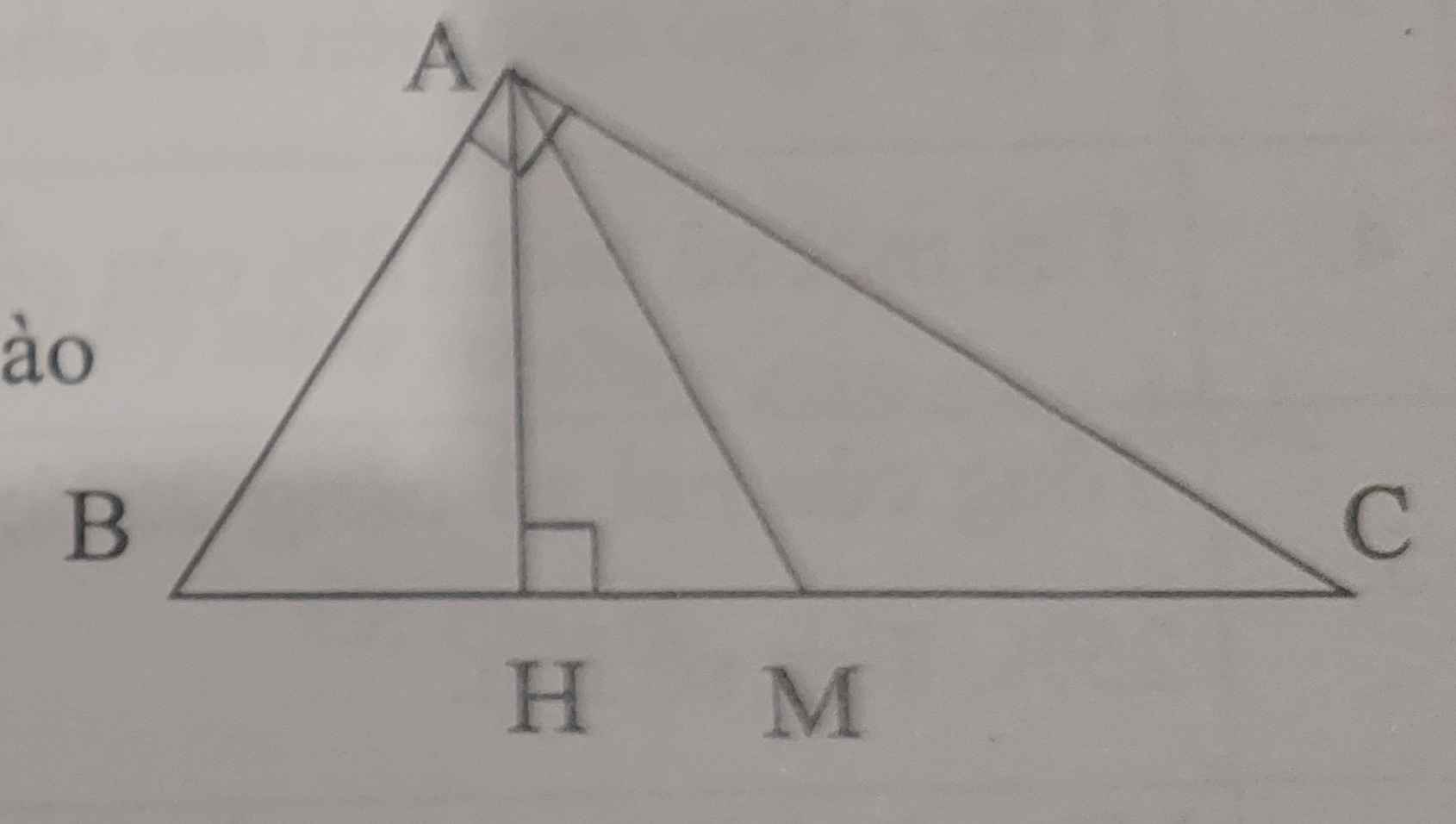
a: ΔABC, ΔAHB,ΔAHM, ΔAMC
b: 1 góc tù: ΔAMC
1 góc vuôg: ΔAHB; ΔAHC
Tam giác ABC(hình bên)có chiều cao AH = 8cm. M là trung điểm của cạnh BC.
A) AH là đường cao của những tấm giác nào?
B) tính dâyd BC, biết diện tích tam giác AMC là 24 cm²
C) tính diện tích tam giác ABC .
a.
AH là đường cao của các tam giác ABC, AMB và AMC
b.
Độ dài cạnh MC là:
\(2\times24:8=6\left(cm\right)\)
Độ dài đáy BC là:
\(6\times2=12\left(cm\right)\)
c.
Diện tích tam giác ABC là:
\(8\times12:2=48\left(cm^2\right)\)
Một hình tam giác có đáy bằng 8 cm, đường cao bằng 4 cm. Vậy diện tích của hình tam giác đó là: A. 6 cm2 B. 16 cm C. 32 cm2 D. 16 cm2
Khoanh vào chữ đặt trước kết quả đúng:
Số hình tam giác có trong hình bên là:
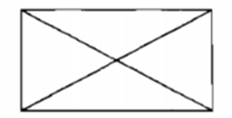
A. 4 B. 6
C. 7 D. 8
Phương pháp giải:
- Đếm các hình tam giác đơn.
- Ghép hình, đếm tiếp cho đến hết tất cả các hình tam giác.
Lời giải chi tiết:
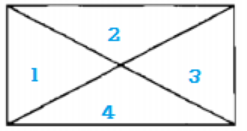
Hình trên có các hình tam giác là: 1; 2; 3; 4; 1+2; 2+3; 3+4; 4 +1.
Chọn đáp án D. 8.
1:Cho tam giác ABC vuông tại A,có:AB=6 cm,AC =8 cm,đường cao AH .Đường phân giác BD cắt AH tại 1 (D ϵAC).
a,Tính độ dài các đoạn thẳng BC,AD và DC.
b,Chứng minh:ΔABD ∼ ΔHBI
2:Cho hình lăng trụ đứng ABCD A'B'C'D'' có ABCD là hình chữ nhật.Tính thể tích của hình lăng trụ,biết AA' =8 cm,AB=3 cm,AC=5 cm
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Vậy: BC=10cm
a) Xét ΔABC có
BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)(Tính chất tia phân giác của tam giác)
hay \(\dfrac{AD}{6}=\dfrac{CD}{10}\)
mà AD+CD=AC=8(cm)(D nằm giữa A và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau,ta được:
\(\dfrac{AD}{6}=\dfrac{CD}{10}=\dfrac{AD+CD}{6+10}=\dfrac{8}{16}=\dfrac{1}{2}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{AD}{6}=\dfrac{1}{2}\\\dfrac{CD}{10}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AD=3\left(cm\right)\\CD=5\left(cm\right)\end{matrix}\right.\)
Vậy: AD=3cm; CD=5cm
b) Xét ΔABD vuông tại A và ΔHBI vuông tại H có
\(\widehat{ABD}=\widehat{HBI}\)(BI là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔABD\(\sim\)ΔHBI(g-g)