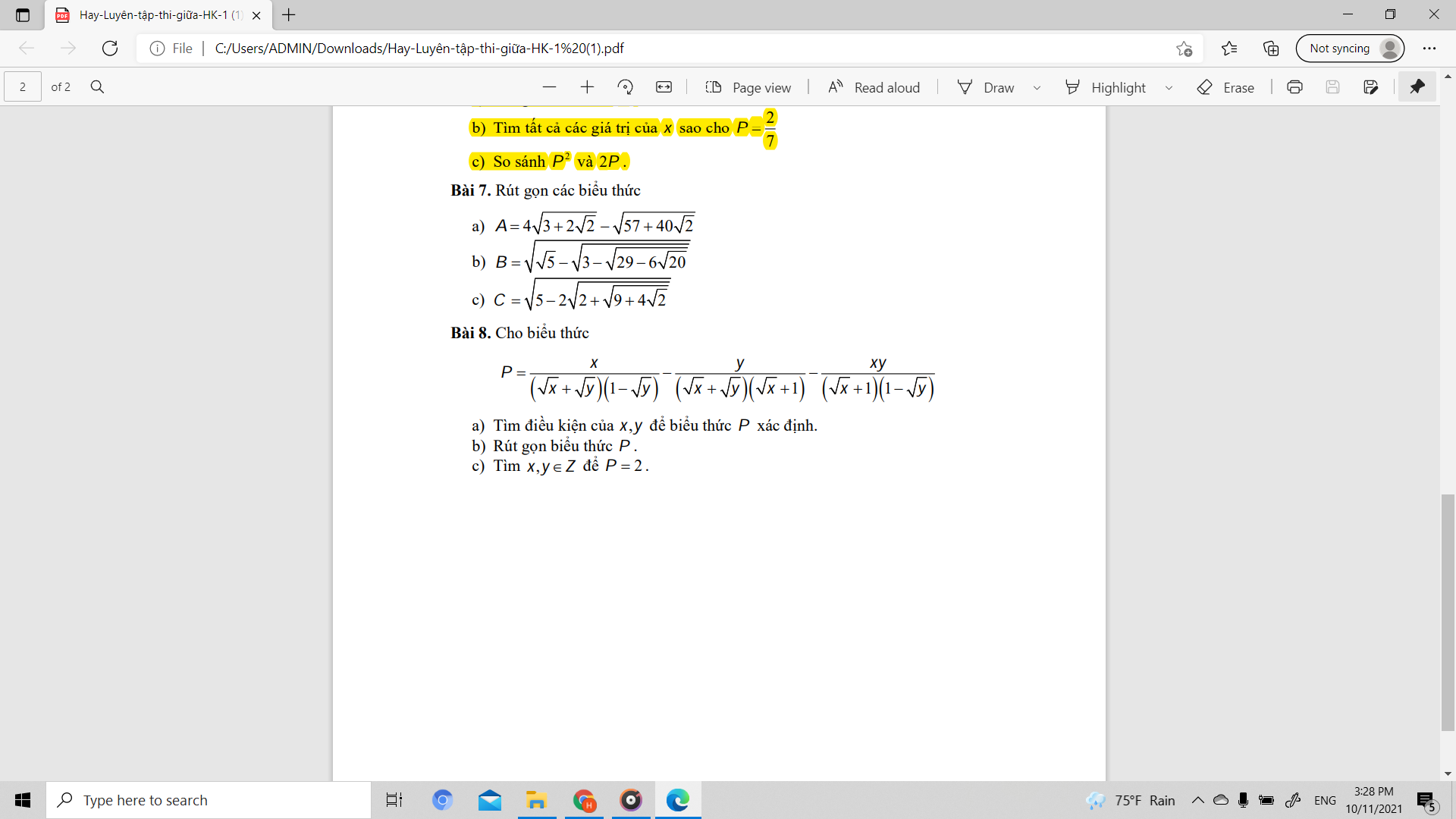
Bài 7:

a: Ta có: \(A=4\sqrt{3+2\sqrt{2}}-\sqrt{57+40\sqrt{2}}\)

\(=4\sqrt{2}+4-4\sqrt{2}-5\)

=-1

Caai 7 :

a) C2H4 + Br2 $\to$ C2H4Br2

b) Theo PTHH : n C2H4 = n Br2 = 8/160 = 0,05(mol)

%V C2H4 = 0,05.22,4/2,24  .100% = 50%

%V CH4 = 100% -50% = 50%

Câu 8 :

a) C2H5OH = a(mol) => n CH3COOH  = 2a(mol)

$C_2H_5OH + Na \to C_2H_5OH + \dfrac{1}{2}H_2$
$CH_3COOH + Na \to CH_3COONa + \dfrac{1}{2}H_2$

Theo PTHH :

n H2 = 1/2 n C2H5OH + 1/2 n CH3COOH = 0,5a + a = 3,36/22,4 = 0,15

=> a = 0,1

=> m = 0,1.46 + 0,1.2.60 = 16,6(gam)

b)

$C_2H_5OH + CH_3COOH \buildrel{{H_2SO_4,t^o}}\over\rightleftharpoons CH_3COOC_2H_5 + H_2O$

Ta thấy : n C2H5OH < n CH3COOH nên hiệu suất tính theo số mol C2H5OH

n CH3COOC2H5 = n C2H5OH pư = 0,1.80% = 0,08(mol)

m este = 0,08.88 = 7,04(gam)

6.C

7.A

8.B

6. Egypt is believed to be the driest country in the world.

7. The Taj is said to have been built with blind people who couldn't see how beautiful it is.

8. He is alleged to have kicked a policeman.

9. The train was supposed to arrive at 11.30.

10. The two injured men are thought to have been repairing overhead cables.

7.

\(\lim\left(3.4^n-5^n\right)=\lim5^n\left(3.\left(\dfrac{4}{5}\right)^n-1\right)=+\infty.\left(-1\right)=-\infty\)

8.

\(\lim\dfrac{n^2+n-1}{3n+2}=\lim\dfrac{n^2\left(1+\dfrac{1}{n}-\dfrac{1}{n^2}\right)}{n\left(3+\dfrac{2}{n}\right)}=\lim\dfrac{n\left(1+\dfrac{1}{n}-\dfrac{1}{n^2}\right)}{3+\dfrac{2}{n}}=\dfrac{+\infty}{3}=+\infty\)

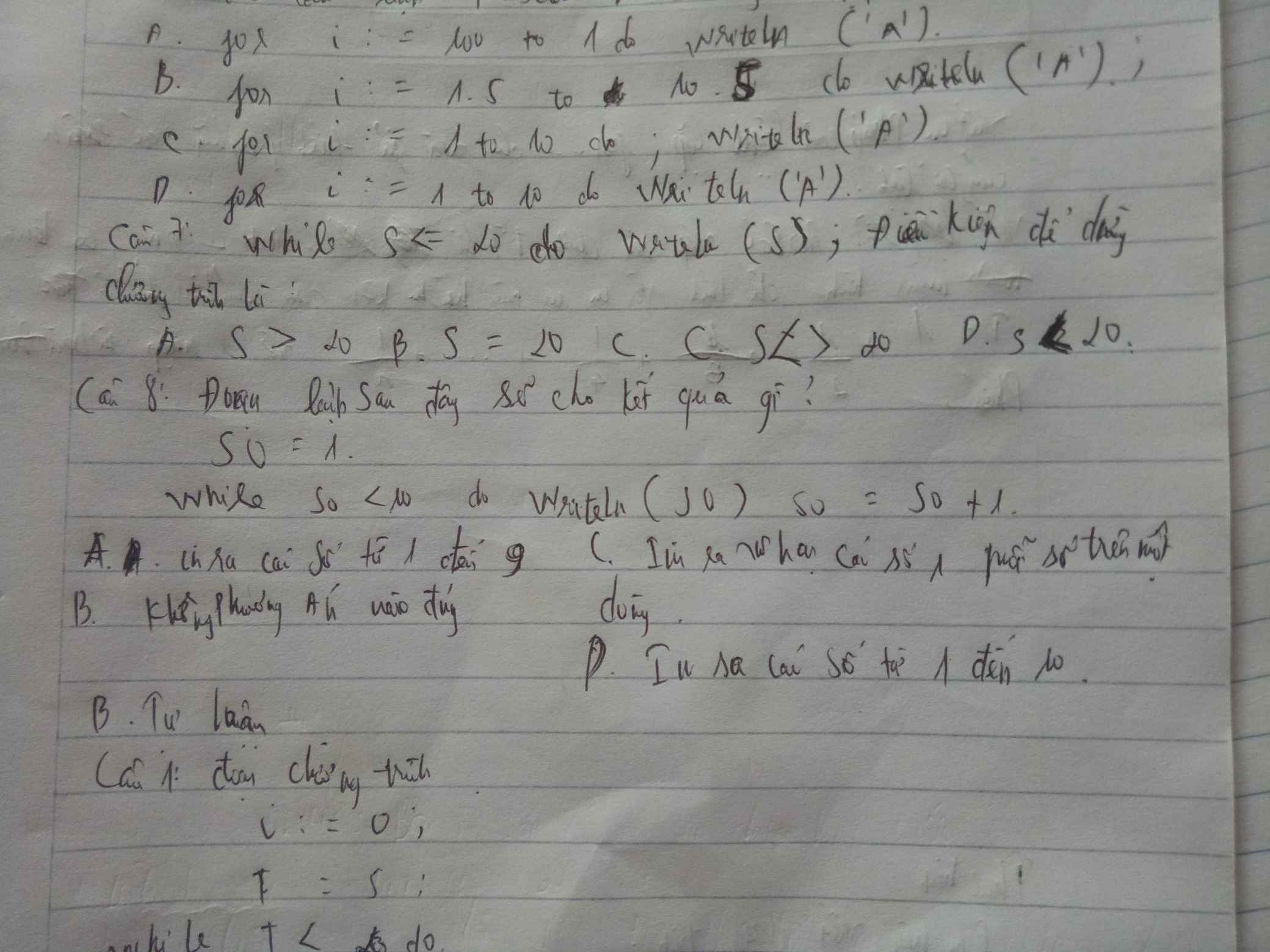
7A

8 Không có begin - end; để bao quát các câu lệnh ở lệnh lặp while do này thì đây là vòng lặp vô hạn bạn nhé. (Mình dịch không được đáp án B nên bạn dựa vào dữ liệu mình cho để khoanh đáp án chính xác nhé)

\(A=x^7-4x^3+x^2+2=x^3\left(x^4-4\right)+x^2+2\)

\(=x^3\left(x^2-2\right)\left(x^2+2\right)+x^2+2\)

\(=\left(x^2+2\right)\left(x^3\left(x^2-2\right)+1\right)\)

\(=\left(x^2+2\right)\left(x^5-2x^3+1\right)\)

\(=\left(x^2+2\right)\left(x^5-x^4+x^4-x^3-x^3+x^2-x^2+x-x+1\right)\)

\(=\left(x^2+2\right)\left[x^4\left(x-1\right)+x^3\left(x-1\right)-x^2\left(x-1\right)-x\left(x-1\right)-\left(x-1\right)\right]\)

\(=\left(x^2+2\right)\left(x-1\right)\left(x^4+x^3-x^2-x-1\right)\)