Cho mặt cầu (S) có tâm I, bán kính R = 5. Một đường thẳng d cắt (S) tại hai điểm M, N phân biệt nhưng không đi qua I. Đặt MN = 2m Với giá trị nào của m thì diện tích tam giác IMN lớn nhất?
A. m = 5 2
B. m = ± 5 2 2
C. m = 5 2 2
D. m = 10 2
Cho mặt cầu (S) có tâm I, bán kính R=5. Một đường thẳng d cắt (S) tại hai điểm M, N phân biệt nhưng không đi qua I. Đặt MN=2m Với giá trị nào của m thì diện tích tam giác IMN lớn nhất?
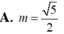
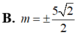
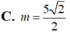
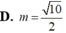
Cho (Cm) là đồ thị của hàm số y = x 3 + 3 m x + 1 (với m ∈ ( - ∞ ; 0 ) là tham số thực). Gọi d là đường thẳng đi qua hai điểm cực trị của (Cm). Tìm số các giá trị của m để đường thẳng d cắt đường tròn tâm I(1;0) bán kính R=3 tại hai điểm phân biệt A, Bsao cho diện tích tam giác IAB đạt giá trị lớn nhất.
A.3
B.0
C.1
D.2
Chọn C
![]() .
.
Vì ![]() nên phương trình
nên phương trình ![]() có 2 nghiệm phân biệt.
có 2 nghiệm phân biệt.
Do đó hàm số có hai điểm cực trị ![]() .
.
Giả sử hàm số có hai điểm cực trị lần lượt là ![]() và
và ![]() , với
, với ![]() ,
, ![]() là nghiệm của phương trình
là nghiệm của phương trình ![]() .
.
Thực hiện phép chia ![]() cho
cho ![]() ta được :
ta được : ![]() .
.
Khi đó ta có: 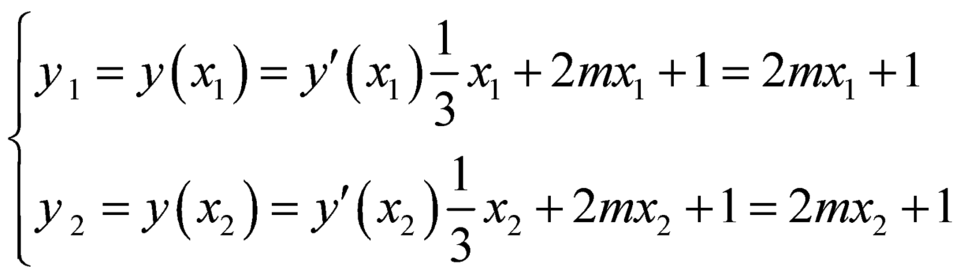 .
.
Ta thấy, toạ độ hai điểm ![]() và
và ![]() thoả mãn phương trình
thoả mãn phương trình ![]() .
.
Do đó, phương trình đường thẳng qua hai điểm cực trị là ![]() .
.
Ta thấy ![]() luôn qua
luôn qua ![]() .
.
Đặt ![]()
![]() .
.
![]() .
.
Xét hàm số ![]() ,
, ![]() .
.
![]() ,
, ![]() .
.
Suy ra hàm số ![]() liên tục và đồng biến trên
liên tục và đồng biến trên ![]() .
.
Do đó ![]() .
.
Vậy ![]() đạt giá trị lớn nhất
đạt giá trị lớn nhất ![]()
![]() .
.
Tìm tất cả các giá trị thực của tham số m để đường thẳng đi qua điểm cực đại, cực tiểu của đồ thị hàm số y = x 3 - 3 m x + 2 cắt đường tròn tâm I(1;1) bán kính R=1 tại hai điểm phân biệt A, B sao cho diện tích tam giác IAB đạt giá trị lớn nhất.
A. m = 2 ± 3 2
B. m = 1 ± 3 2
C. m = 2 ± 5 2
D. m = 1 ± 5 2
Cho mặt cầu tâm O bán kính r. Gọi ( α ) là mặt phẳng cách tâm O một khoảng h (0 < h < r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng ( α ) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Với vị trí nào của CD thì diện tích tam giác BCD lớn nhất?
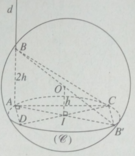
Diện tích tam giác BCD bằng:
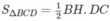
Diện tích này lớn nhất khi AI // CD.
Gọi m 0 là giá trị của tham số m để đường thẳng đi qua điểm cực đại và cực tiểu của đồ thị hàm số y = x 3 - 6 m x + 4 cắt đường tròn tâm I(1;0), bán kính bằng 2 tại hai điểm phân biệt A, B sao cho diện tích tam giác IAB đạt giá trị lớn nhất. Mệnh đề nào sau đây đúng:
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị của m để đường thẳng đi qua điểm cực đại, cực tiểu của đồ thị hàm số y = x 3 − 3 m x + 2 cắt đường tròn tâm I 1 ; 1 , bán kính bằng 1 tại hai điểm phân biệt sao cho diện tích tam giác IAB đạt giá trị lớn nhất
A. m = 1 ± 3 2
B. m = 2 ± 3 2
C. m = 2 ± 5 2
D. m = 2 ± 3 3
Trong mặt phẳng Oxy, cho đường tròn (C): x2+y2-2x-2y-14=0 và điểm A(2;0). Gọi I là tâm của (C). Viết pt đường thẳng đi qua A và cắt (C) tại hai điểm M, N sao cho tam giác IMN có diện tích lớn nhất.
Trong mặt phẳng Oxy,cho đường tròn (C):x2+y2-2x-2y-14=0 và điểm A(2;0).Gọi I là tâm của (C).Viết phương trình đường thẳng đi qua A và cắt (C) tại hai điểm M,N sao cho tam giác IMN có diện tích lớn nhất
Đề của sở hả bạn ? ( hình như bài này còn cách khác nữa ...)
( hình như bài này còn cách khác nữa ...)
Trong mặt phẳng Oxy, cho đường tròn ( C ) : x2+y2-2x-2y-14=0 và điểm A(2;0) . gọi I là tâm của ( C ). Viết phương trình đường thẳng đi qua A và cắt ( C ) tại hai diểm M,N sao cho tam giác IMN có diện tích lớn nhất
Đường tròn (C) tâm \(I\left(1;1\right)\) bán kính \(R=4\)
\(\overrightarrow{IA}=\left(1;-1\right)\Rightarrow IA=\sqrt{2}\) (chà, rắc rối rồi, do \(\dfrac{IA}{R}< \dfrac{\sqrt{2}}{2}\) nên tam giác IMN không bao giờ có thể vuông được)
Ta có: \(S_{\Delta IMN}=\dfrac{1}{2}IM.IN.sin\widehat{MIN}=\dfrac{1}{2}R^2.sin\widehat{MIN}\)
\(\Rightarrow S_{IMN-max}\) khi \(sin\widehat{MIN}\) đạt max
Gọi H là trung điểm MN \(\Rightarrow IH\perp MN\Rightarrow IH\le IA\)
Do vai trò M, N là như nhau, không mất tính tổng quát, giả sử M, H nằm cùng phía so với A
\(cos\widehat{MIH}=\dfrac{IH}{IM}\le\dfrac{IA}{IM}=\dfrac{\sqrt{2}}{4}\Rightarrow\widehat{MIH}\ge69^018'\) (do \(0< \widehat{MIH}\le90^0\) nên \(cos\widehat{MIH}\) nghịch biến so với \(\widehat{MIH}\))
\(\Rightarrow\widehat{MIN}=2\widehat{MIH}>90^0\Rightarrow sin\widehat{MIN}\) nghịch biến so với \(\widehat{MIN}\)
\(\Rightarrow sin\widehat{MIN}_{max}\) khi \(\widehat{MIN}_{min}\)
Lại có: \(\widehat{MIN}=180^0-2.\widehat{IMH}\Rightarrow\widehat{MIN}_{min}\) khi \(\widehat{IMH}_{max}\)
\(\Rightarrow sin\widehat{IMH}_{max}\) (\(0\le\widehat{IMH}\le90^0\) nên \(sin\widehat{IMH}\) và \(\widehat{IMH}\) đồng biến)
\(sin\widehat{IMH}=\dfrac{IH}{IM}\le\dfrac{IA}{IM}\Rightarrow sin\widehat{IMH}_{max}\) khi H trùng A
Hay \(S_{\Delta IMN-max}\) khi H trùng A \(\Leftrightarrow d\perp IA\)
\(\Rightarrow d\) nhận (1;-1) là 1 vtpt
Phương trình d: \(1\left(x-2\right)-y=0\Leftrightarrow x-y-2=0\)