Cho hình hộp chữ nhật có diện tích của ba mặt lần lượt là 60 c m 2 , 72 c m 2 , 81 c m 2 . Khi đó thể tích Vcủa khối hình hộp chữ nhật gần nhất với giá trị nào sau đây?
A. 595.
B. 592.
C. 593.
D. 594.
Cho hình hộp chữ nhật có diện tích của ba mặt lần lượt là 60 c m 2 , 72 c m 2 , 81 c m 2 . Khi đó thể tích V của khối hình hộp chữ nhật gần nhất với giá trị nào sau đây?
A. 595.
B. 592.
C. 593.
D. 594.
Chọn B.
Giả sử khối hộp chữ nhật có ba kích thước là a, b, c.
Khi đó thể tích khối hộp chữ nhật là: V = abc.
Từ giả thiết ta có
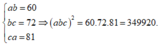
![]()
Vậy thể tích V của khối hình hộp chữ nhật gần nhất với giá trị 592.
Một hình hộp chữ nhật có ba kích thước lần lượt là a, b, c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Diện tích của mặt cầu (S) theo a, b, c là:
A. π ( a 2 + b 2 + c 2 ) B. 2 π ( a 2 + b 2 + c 2 )
C. 4 π ( a 2 + b 2 + c 2 ) D. π /2.( a 2 + b 2 + c 2 )
Chọn A.
Đường kính của mặt cầu (S) chính là đường chéo của hình hộp chữ nhật, nên mặt cầu (S) có bán kính
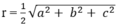
Do đó diện tích mặt cầu (S) là: S = 4 πr 2 = π( a 2 + b 2 + c 2 )
Ba mặt qua cùng một đỉnh của một hình hộp chữ nhật có diện tích lần lượt là 12 c m 2 , 18 c m 2 và 24 c m 2 . Thể tích hình hộp chữ nhật này là
A. 72 c m 3 .
B. 52 c m 3 .
C. 48 c m 3 .
D. 36 c m 3 .
Đáp án A
Gọi chiều dài, rộng và cao của hình hộp chữ nhật lần lượt là a;b;c . Ta có a b = 12 b c = 18 c d = 24 ⇒ a b c = 72
Thể tích hình hộp là V = a b c = 72 c m 3
Ba mặt qua cùng một đỉnh của một hình hộp chữ nhật có diện tích lần lượt là 12 c m 2 , 18 c m 2 và 24 c m 2 Thể tích hình hộp chữ nhật này là
![]()
![]()
![]()
![]()
Diện tích ba mặt của hình hộp chữ nhật lần lượt bằng 20 c m 3 , 28 c m 3 , 35 c m 3 . Thể tích của hình hộp đó bằng
![]()
![]()
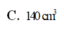
![]()
Diện tích ba mặt của hình hộp chữ nhật lần lượt bằng 20 c m 3 , 28 c m 3 , 35 c m 3 . Thể tích của hình hộp đó bằng
A. 165 c m 3
B. 190 c m 3
C. 140 c m 3
D. 160 c m 3
Đáp án C
Gọi kích thước 3 cạnh của hình hộp chữ nhật là a,b,c cm. Theo giả thiết, ta có
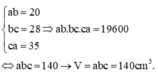
Cho hình hộp chữ nhật ABCD.A'B'C'D' có diện tích các mặt ABCD, BCC'B', CDD'C' lần lượt là 2a2, 3a2, 6a2. Tính thể tích khối hộp chữ nhật ABCD.A'B'C'D'.
A. 36a3
B. 6a3
C. 36a6
D. 6a2
Đáp án B
Ta đặt AB=x, AD=y, AA'=z. Khi đó theo giả thiết ta có:
x y = 2 a 2 x z = 3 a 2 y z = 6 a 2 ⇔ x y = 2 a 2 x z = 3 a 2 y z = 6 a 2 x y z = 6 a 3 ⇔ x = a y = 2 a z = 3 a
Vậy thể tích khối hôp chữ nhật V=6a3.
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có diện tích các mặt A B C D , B C C ' B ' , C D D ' C ' lần lượt là 2 a 2 , 3 a 2 , 6 a 2 . Tính thể tích khối hộp chữ nhật A B C D . A ' B ' C ' D ' .
A. 36 a 3
B. 6 a 3
C. 36 a 6
D. 6 a 2
Đáp án B
Gọi độ dài 3 chiều của hình hộp lần lượt là x;y;z . ta có: x y = 2 a 2 y z = 3 a 2 ⇒ x y z = 6 a 3 z x = 6 a 2
Thể tích khối tứ diện là: V = x y z = 6 a 3
Cho khối hộp chữ nhật A B C D A ' B ' C ' D ' . Gọi M là trung điểm của BB'. Mặt phẳng M D C ' chia khối hộp chữ nhật thành hai khối đa diện, một khối chứa đỉnh C và một khối chứa đỉnh A'. Gọi V 1 , V 2 lần lượt là thể tích hai khối đa diện chứa C và A'. Tính V 1 V 2 .
A. V 1 V 2 = 7 24
B. V 1 V 2 = 7 17
C. V 1 V 2 = 7 12
D. V 1 V 2 = 17 24
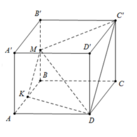
Chuẩn hóa hình hộp đã cho là hình lập phương cạnh a.
Dựng M K / / A B ' / / C ' D
Khi đó thiết diện là tứ giác
Ta có: V 1 = 1 3 h S 1 + S 1 S 2 + S 2
Trong đó h = H B = a ' S 1 = S B M K = a 2 8 ; S 2 = S C ' D C = a 2 2
Do đó V 1 = 7 24 a 3 ⇒ V 2 = a 3 − V 1 = 17 24 a 3
Vậy V 1 V 2 = 7 17
Đáp án B