Dùng bảng căn bậc hai, tìm giá trị gần đúng của nghiệm phương trình
x 2 = 0 , 3982 .
Những câu hỏi liên quan
Dùng bảng căn bậc hai, tìm giá trị gần đúng của nghiệm phương trình
x2 = 0,3982.
x2 = 0,3982 ⇔ x = ±√0,3982
Ta có: 0,3982 = 39,82:100
Do đó: √0,3982 = √39,82 : √100 = 6,310 : 10 = 0,631
Vậy x = ±0,631
Đúng 0
Bình luận (0)
Dùng bảng căn bậc hai để tìm giá trị gần đúng của nghiệm mỗi phương trình sau:
x2 = 3,5
x2 = 3,5 ⇔ x = ±√3,5
Tra bảng ta được: √3,5 ≈ 1,871
Vậy phương trình có hai nghiệm: x = ±1,871
x1= 1,871; x2 = -1,871
Đúng 0
Bình luận (0)
Dùng bảng căn bậc hai để tìm giá trị gần đúng của nghiệm mỗi phương trình sau: x2 = 132
x2 = 132 ⇔ x = ±√132 = ±√1,32.√100 = ±10√1,32
Tra bảng ta được: √1,32 ≈ 1,149 nên
10√1,32 ≈ 10.1,149 ≈ 11,49
Vậy phương trình có hai nghiệm: x = ±11,49
Đúng 0
Bình luận (0)
Dùng bảng căn bậc hai để tìm giá trị gần đúng của nghiệm mỗi phương trình sau:
a ) x 2 = 3 , 5 ; b ) x 2 = 132
a) x 2 = 3 , 5 ⇔ x = ± √ 3 , 5
Tra bảng ta được: √3,5 ≈ 1,871
Vậy phương trình có hai nghiệm: x = ±1,871
x 1 = 1 , 871 ; x 2 = - 1 , 871
b) x 2 = 132 ⇔ x = ± √ 132 = ± √ 1 , 32 . √ 100 = ± 10 √ 1 , 32
Tra bảng ta được: √1,32 ≈ 1,149 nên
10√1,32 ≈ 10.1,149 ≈ 11,49
Vậy phương trình có hai nghiệm: x = ±11,49
Đúng 0
Bình luận (0)
Dùng bảng căn bậc hai để tìm giá trị gần đúng của nghiệm mỗi phương trình sau :
a) \(x^2=3,5\)
b) \(x^2=132\)
Dùng máy tính bỏ túi, tính giá trị gần đúng của nghiệm mỗi phương tình sau (làm tròn đến chữ số thập phân thứ ba):
a
)
x
2
2
;
b
)
x
2
3
c
)
x
2
3
,
5...
Đọc tiếp
Dùng máy tính bỏ túi, tính giá trị gần đúng của nghiệm mỗi phương tình sau (làm tròn đến chữ số thập phân thứ ba):
a ) x 2 = 2 ; b ) x 2 = 3 c ) x 2 = 3 , 5 ; d ) x 2 = 4 , 12
Hướng dẫn: Nghiệm của phương trình x 2 = a ( với a ≥ 0) là các căn bậc hai của a.
a) x 2 = 2 = > x 1 = √ 2 v à x 2 = - √ 2
Dùng máy tính bỏ túi ta tính được:
√ 2 ≈ 1 , 414213562
Kết quả làm tròn đến chữ số thập phân thứ ba là:
x 1 = 1 , 414 ; x 2 = - 1 , 414 b ) x 2 = 3 = > x 1 = √ 3 v à x 2 = - √ 3
Dùng máy tính ta được:
√ 3 ≈ 1 , 732050907
Vậy x 1 = 1 , 732 ; x 2 = - 1 , 732
c) x 2 = 3 , 5 = > x 1 = √ 3 , 5 v à x 2 = - √ 3 , 5
Dùng máy tính ta được:
√ 3 , 5 ≈ 1 , 870828693
Vậy x 1 = 1 , 871 ; x 2 = - 1 , 871
d) x 2 = 4 , 12 = > x 1 = √ 4 , 12 v à x 2 = - √ 4 , 12
Dùng máy tính ta được:
√ 4 , 12 ≈ 2 , 029778313
Vậy x 1 = 2 , 030 ; x 2 = - 2 , 030
Đúng 0
Bình luận (0)
Bài 3 (trang 6 SGK Toán 9 Tập 1)
Dùng máy tính bỏ túi, tính giá trị gần đúng của nghiệm mỗi phương tình sau (làm tròn đến chữ số thập phân thứ ba):
a) $x^2 = 2$; b) $x^2 = 3$;
c) $x^2 = 3,5$; d) $x^2 = 4,12$.
Hướng dẫn:
Nghiệm của phương trình $x^2 = a$ ( với $a \ge 0$) là các căn bậc hai của $a$.
\(a)x^2=2\Rightarrow x_1=\sqrt{2}\) và \(x_2=-\sqrt{2}\)
Dùng máy tính bỏ túi ta tính được:
\(\sqrt{2}\text{≈}1,414213562\)
Kết quả làm tròn đến chữ số thập phân thứ ba là:
\(x_1=1,414;x_2=-1414\)
\(b)x^2=3\Rightarrow x_1=\sqrt{3}\)và \(x_2=-\sqrt{3}\)
Dùng máy tính ta được:
\(\sqrt{3}\text{≈ 1,732050907}\)
Vậy \(x_1=1,732;x_2=-1,732\)
\(c)x^2=3,5\Rightarrow x_1=\sqrt{3,5}\)và \(x_2=-\sqrt{3,5}\)
Dùng máy tính ta được:
\(\sqrt{3,5}\text{≈ 1,870828693}\)
Vậy \(x_1=1,871;x_2=-1,871\)
\(d)x^2=4,12\Rightarrow x_1=\sqrt{4,12}\)và \(x_2=-\sqrt{4,12}\)
Dùng máy tính ta được:
\(\sqrt{4,2}\text{≈ 2,029778313}\)
Vậy \(x_1=2,030;x_2=-2,030\)
a) x = \(\sqrt{2}\)
b) x = \(\sqrt{3}\)
c) x = \(\dfrac{\sqrt{14}}{2}\)
d)x = \(\dfrac{\sqrt{103}}{5}\)
a) x2 = 2
=> √x2 = √2
<=> |x| = √2
<=> x = +- √2 ≈ +- 1.414
b) x2 = 3
=> |x| = √3
<=> x = +-√3 ≈ +- 1.732
c) x2 = 3.5
=> |x| = √3.5
<=> x = +- √3.5 ≈ +- 1.871
d) x2 = 4.12
=> |x| = √4.12
<=> x = +- √4.12 ≈ +- 2.030
Xem thêm câu trả lời
Cho phương trình
1
2
x
2
-
2
x
+
1
0
Vẽ các đồ thị của hai hàm số
y
1
2
x
2...
Đọc tiếp
Cho phương trình 1 2 x 2 - 2 x + 1 = 0
Vẽ các đồ thị của hai hàm số y = 1 2 x 2 , y = 2x – 1 trong cùng một mặt phẳng tọa độ. Dùng đồ thị tìm giá trị gần đúng nghiệm của phương trình (làm tròn đến chữ số thập phân thứ hai)
*Vẽ đồ thị hàm số y = 1 2 x 2
| x | -2 | -1 | 0 | 1 | 2 |
| y = 1 2 x 2 | 2 | 1/2 | 0 | 1/2 | 2 |
*Vẽ đồ thị hàm số y = 2x – 1
Cho x = 0 thì y = -1 ⇒ (0; -1)
Cho y = 0 thì x = 1/2 ⇒ (1/2 ; 0)
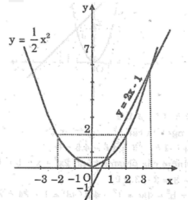
Dựa vào đồ thị, ta có : x 1 ≈ 0 , 60 , x 2 ≈ 3 , 40
Đúng 0
Bình luận (0)
Tìm giá trị gần đúng của căn bậc ba mỗi số sau bằng bảng lập phương và kiểm tra bằng máy tính bỏ túi (làm tròn đến chữ số thập phân thứ ba): 25,3