+) Xét tam giác SAC có SA = SC \( \Rightarrow \) SAC là tam giác cân mà SO là trung tuyến

\( \Rightarrow \) SO \( \bot \) AC.

Xét tam giác SBD có SB = SD \( \Rightarrow \) SBD là tam giác cân mà SO là trung tuyến

\( \Rightarrow \) SO \( \bot \) BD.

+) Ta có SO \( \bot \) AC; SO \( \bot \) BD; AC \( \cap \) BD tại O \( \Rightarrow \) SO \( \bot \) (ABCD).

cái lon cc

Lời giải:

Vì $ABCD$ là hình bình hành nên tâm $O$ là trung điểm $AC$

$\Rightarrow OK$ là đường trung bình của $SAC$ ứng với cạnh $SA$

$\Rightarrow OK\parallel SA$

Mà $SA\subset (SAB)$ nên $OK\parallel (SAB)$

Câu 1: giả sử:\(\overrightarrow{BD}-\overrightarrow{BA}=\overrightarrow{OC}-\overrightarrow{OB}\Leftrightarrow\overrightarrow{BA}+\overrightarrow{AD}-\overrightarrow{BA}=\overrightarrow{OC}+\overrightarrow{BO}\)

\(\Leftrightarrow\overrightarrow{AD}=\overrightarrow{BC}\)(luôn đúng vì ABCD lad hình bình hành)

giả sử: \(\overrightarrow{BC}-\overrightarrow{BD}+\overrightarrow{BA}=\overrightarrow{0}\Leftrightarrow\overrightarrow{BC}-\overrightarrow{BC}+\overrightarrow{DC}+\overrightarrow{BA}=\overrightarrow{0}\)

\(\Leftrightarrow\overrightarrow{BB}+\overrightarrow{DD}=\overrightarrow{0}\)(LUÔN ĐÚNG)

câu 2 :GIẢ SỬ:

 \(\overrightarrow{AB}+\overrightarrow{OA}=\overrightarrow{OB}\Leftrightarrow\overrightarrow{AO}+\overrightarrow{OB}+\overrightarrow{OA}+\overrightarrow{BO}=\overrightarrow{0}\)(luôn đúng)

giả sử: \(\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}\\ \Leftrightarrow\overrightarrow{MB}+\overrightarrow{BA}+\overrightarrow{MD}+\overrightarrow{DC}=\overrightarrow{MB}+\overrightarrow{MD}\Leftrightarrow\overrightarrow{0}=\overrightarrow{0}\)

a) Ta có AB = CD (cạnh hình thoi)

BE = DG (gt)

⇒ AB + BE = CD + DG hay AE = CG (cmt)

Xét ΔAHE và ΔCFG có:

AE = CG

∠HAE = ∠FCG (cùng bù với ∠BAD = ∠DCB ),

AH = CF (gt)

Do đó ΔAHE = ΔCFG (c.g.c) ⇒ HE = FG

Chứng minh tương tự ta có HG = EF

Do đó tứ giác EFGH là hình bình hành (các cạnh đối bằng nhau).

b) Nối E và G.

Xét ΔOBE và ΔODG có

BE = DG (gt),

∠OBE = ∠ODG (so le trong),

OB = OD ( tính chất đường chéo của hình thoi ABCD)

⇒ ΔOBE = ΔODG (c.g.c) ⇒ ∠OBE = ∠ODG

Mà ∠DOG + ∠GOB = 180o ⇒ ba điểm G, O, E thẳng hàng.

Chứng minh tương tự ta có H, O, F thẳng hàng.

Vậy O là tâm đối xứng của hình bình hành EFGH.

c) Hình bình hành EFGH là hình thoi ⇔ HE = EF

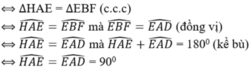
⇔ Hình thoi ABCD có 1 góc vuông

⇔ ABCD là hình vuông.

Vậy hình thoi ABCD phải là hình vuông thì hình bình hành EFGH trở thành hình thoi.

a) Do các tứ giác ABCD và ABEF là các hình bình hành

=> O là trung điểm của AC và BD

và O’ là trung điểm của AE và BF. (tính chất hình bình hành).

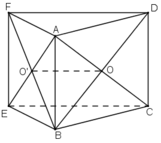
+ ΔBFD có OO’ là đường trung bình nên OO’ // DF

mà DF ⊂ (ADF)

⇒ OO' // (ADF)

+ ΔAEC có OO’ là đường trung bình nên OO’ // EC

mà EC ⊂ (BCE)

⇒ OO’ // (BCE).

b)

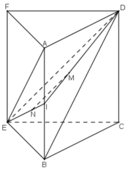
Ta thấy mp(CEF) chính là mp(CEFD).

Gọi I là trung điểm của AB:

+ M là trọng tâm ΔABD

⇒ IM/ ID = 1/3.

+ N là trọng tâm ΔABE

⇒ IN/IE = 1/3.

+ ΔIDE có IM/ID = IN/IE = 1/3

⇒ MN // DE mà ED ⊂ (CEFD)

nên MN // (CEFD) hay MN // (CEF).