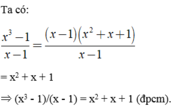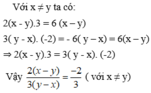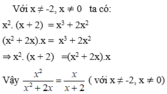Chứng minh các đẳng thức sau: x 6 x + 2 x 3 + 6 x : 6 x = 2 1 3 v ớ i x > 0

Những câu hỏi liên quan
Chứng minh các bất đẳng thức sau: tan x > x 0 < x < π 2
Xét hàm số y = f(x) = tanx – x trên khoảng (0; π/2)
Ta có: y’ = 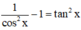 > 0 với ∀ x ∈ R.
> 0 với ∀ x ∈ R.
⇒ hàm số đồng biến trên khoảng (0; π/2)
⇒ f(x) > f(0) = 0 với ∀ x > 0
hay tan x – x > 0 với ∀ x ∈ (0; π/2)
⇔ tan x > x với ∀ x ∈ (0; π/2) (đpcm).
Đúng 0
Bình luận (0)
Chứng minh các đẳng thức sau x 2 ( x + 2 ) x ( x + 2 ) = x x + 2
Chứng minh các bất đẳng thức sau: \(\dfrac{x^2+1}{x}\ge2\)
BĐT này sai nha bạn.
Nó chỉ đúng khi \(x>0\)
Đúng 1
Bình luận (1)
Với \(x>0\) thì bất đẳng thức tương đương với \(x^2+1\ge2x\)
\(\Leftrightarrow x^2-2x+1\ge0\) \(\Leftrightarrow\left(x-1\right)^2\ge0\) (luôn đúng)
\(\Rightarrow\) Điều cần chứng minh là đúng
Đúng 2
Bình luận (0)
Chứng minh các đẳng thức sau: ( x 3 - 1 ) ( x - 1 ) = x 2 + x + 1
Chứng minh các bất đẳng thức sau: tan x > x + x 3 3 0 < x < π 2
Xét hàm số y = g(x) = tanx - x - 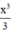 trên
trên 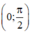
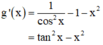
Theo kết quả câu a): tanx > x ∀ x ∈ 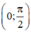
⇒ g'(x) > 0 ∀ x ∈ 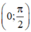
⇒ y = g'(x) đồng biến trên 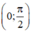
⇒ g(x) > g(0) = 0 với ∀ x ∈ 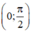
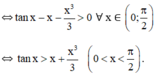
Đúng 0
Bình luận (0)
Chứng minh các đẳng thức sau: 2 ( x - y ) 3 ( y - x ) = - 2 3 ( v ớ i x ≠ y )
chứng minh các đẳng thức sau
(x+y)2+(x-y)2=2(x2+y2)
\(\left(x+y\right)^2+\left(x-y\right)^2=2\left(x^2+y^2\right)\)
\(\Leftrightarrow x^2+2xy+y^2+x^2-2xy=2\left(x^2+y^2\right)\)
\(\Leftrightarrow2x^2+2y^2=2\left(x^2+y^2\right)\left(đúng\right)\)
Đúng 1
Bình luận (0)
chứng minh các đẳng thức sau
(x+y)2+(x-y)2=2(x2+y2)
Chứng minh các đẳng thức sau: x 2 x 2 + 2 x = x x + 2 ( v ớ i x ≠ - 2 , x ≠ 0 )
Chứng minh các bất đẳng thức sau: \(\dfrac{x^2+1}{x}\ge2\left(x\ne0\right)\)
\(\dfrac{x^2+1}{x}=\dfrac{x^2}{x}+\dfrac{1}{x}=x+\dfrac{1}{x}\)
Theo bất đẳng thức Cô - si, ta có:
\(x+\dfrac{1}{x}\ge2\sqrt{x.\dfrac{1}{x}}=2\sqrt{1}=2\)
Vậy \(\dfrac{x^2+1}{x}\ge2\)
Đúng 4
Bình luận (0)
1 cách chứng minh khác (chứng minh tương đương)
\(\dfrac{x^2+1}{x}\ge2\\ \Leftrightarrow x^2+1\ge2x\\ \Leftrightarrow x^2-2x+1=\left(x-1\right)^2\ge0\left(\text{luôn đúng}\right)\)
Vậy BĐT ban đầu được chứng minh
Đúng 3
Bình luận (0)