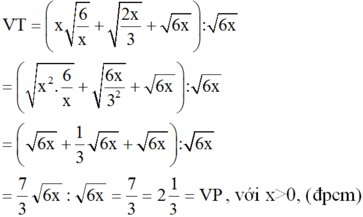Các câu hỏi tương tự
Chứng minh các đẳng thức sau:
a) \(\frac{3}{2}\sqrt{6}+2\sqrt{\frac{2}{3}}-4\sqrt{\frac{3}{2}}=\frac{\sqrt{6}}{6}\)
b) \(\left(x\sqrt{\frac{6}{x}}+\sqrt{\frac{2X}{3}}+\sqrt{6X}\right):\sqrt{6X}=2\frac{1}{3}\)với x > 0
Tìm x, y thỏa mãn các đẳng thức: x^3 + y^3 - 8xy√2(x^2 + y^2) + 7x^2y + 7xy^2 = 0 và √y - √(2x - 3) + 2x = 6
Cho a+b+c=6. Chứng minh 1 trong 3 pt sau có nghiệm: x^2+ax+1=0 ; x^2+bx+1 = 0 ; x^2+cx+1 = 0
Chứng minh các bất đẳng thức sau bắng cách xét tứng khoảng giá trị của biến
a, \(x^4+x^3+x^2+x+1>0\)
b, \(x^8-x^7+x^4+1>0\)
áp dụng bất đẳng thức giải pt sau
\(6\sqrt[3]{x^3+2x^2+2x+2}=x^2+9x+19\)
rút gọn biểu thức chứa căn thức bậc hai
√x/√x-1 - 6/√x-1 - 2√3/√x-1 (x>=0,xkhasc1 )
3-√x/√x-2 - 1-√x/√x-2 - -5√x/√x -2
2-6√x/√x-4 - 1-√x/√x-4 - 3-√x/√x-4
Cho x+y+z=3 . Chứng minh bất đẳng thức
x2 +y2 +z2 +xy+xz+yz lớn hơn hoặc bằng 6
b) Cho 3 số dương x,y,z thỏa mãn điều kiện x+y+z=3/4. Chứng minh:
\(6\left(x^2+y^2+z^2\right)+10\left(xy+yz+zx\right)+2\left(\frac{1}{2x+y+z}+\frac{1}{x+2y+z}+\frac{1}{x+y+2z}\right)\ge9\)
Đẳng thức xảy ra khi nào?
Cho biểu thức A=\(\dfrac{6-2\sqrt{x}}{\sqrt{x}-5}\) và B=\(\dfrac{1}{\sqrt{x}-5}-\dfrac{x+3\sqrt{x}}{25-x}\)với x>0, x # 25.
1) Tính giá trị biểu thức A khi x =16.
2) Chứng minh rằng A +B là một số nguyên.
Gỉai các phương trình sau
a) 5/-x^2+5x-6 + x+3/2-x = 0
b) x/2x+2 - 2x/x^2-2x-3 = x/6-2x
c) 1/x-1 - 3x^2/x^3-1 = 2x/x^2+x+1
d) x+25/2x^2-50 - x+5/x^2-5x = 5-x/2x^2+10x