b: AB=10cm

\(BC=5\sqrt{3}\left(cm\right)\)

\(\widehat{C}=60^0\)

(Lưu ý: ΔABC vuông tại A nên  ∠ B   +   ∠ C   =   90 °

Giải tam giác tức là đi tìm số đo các cạnh và các góc còn lại.)

a)

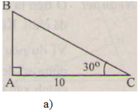
∠ B   =   90 o   -   ∠ C   =   90 °   -   30 °   =   60 °

c   =   b . t g C   =   10 . t g   30 °   ≈   5 , 77   ( c m )

b)

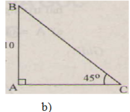
∠ B   =   90 °   -   ∠ C   =   90 °   -   45 °   =   45 °

=> ΔABC cân => b = c = 10 (cm)

c)

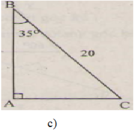
∠ B   =   90 o   -   ∠ C   =   90 °   -   35 °   =   55 °   b   =   a sin B   =   20 . sin 35 °   ≈   11 , 47   ( c m )     c   =   a sin C   =   20 . sin 55 °   ≈   16 , 38   ( c m )

d)

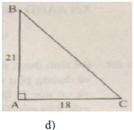
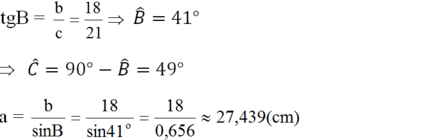
(Ghi chú: Bạn nên sử dụng các kí hiệu cạnh là a, b, c (thay vì BC, AC, AB) để đồng bộ với đề bài đã cho.

Cách để nhớ các cạnh là: cạnh nào thiếu chữ cái nào thì chữ cái đó là kí hiệu của cạnh đó. Ví dụ: cạnh AB thiếu chữ cái C nên c là kí hiệu của cạnh.

hoặc cạnh đối diện với góc nào thì đó chính là kí hiệu của cạnh. Ví dụ: cạnh đối diện với góc B là cạnh b (chính là cạnh AC))

75 đoán bừa vậy!!! hihi

75 cũng đoán bừa

Ta có : \(sinC=\frac{AB}{BC}=\frac{1}{2}\) nên \(BC=2AB=6\)

Suy ra , \(AC=\sqrt{BC^2-AB^2}=3\sqrt{3}\) và góc \(B=60^0\)

****

xét tam giác vuông ABC:

góc A+góc B+góc c=180 độ

90 độ+góc B+30 độ=180 độ

120 độ+góc B=180 độ

góc B=180-120

góc B=60 độ

tick nha

AB = 5 cm, BC=15cm

Ta co tinh chat canh doi dien voi goc 30do thi =1/2 canh huyen.o bai nay thi ta giai nhu sau.goi BC=a=>AB=a/2.ap dung PYTAGO =>(a/2)^2+100=a^2=>a= 11,55

giống toán 9 hơn bạn xem lại ik

minh hok lop 6 thoi

ΔABC(góc A =90⁰)

ta có:góc B+gócC=90⁰ độ(hai góc phụ nhau)

suy ra góc B=90⁰ trừ góc C

                    =90⁰-30⁰=60⁰

suy ra gócB bằng 60⁰

lại có :AB=AC.tan30⁰=10.tan30^o

\(\approx5,774\left(cm\right)\)

có BC=\(\dfrac{AC}{\cos30^0}\)

\(\approx11,547\)

Ta có: ΔABC vuông tại A(gt)

nên \(\widehat{B}+\widehat{C}=90^0\)

hay \(\widehat{B}=60^0\)

Xét ΔABC vuông tại A có 

\(AB=AC\cdot\tan30^0\)

\(\Leftrightarrow AB=10\cdot\dfrac{\sqrt{3}}{3}=\dfrac{10\sqrt{3}}{3}\left(cm\right)\)

Xét ΔABC vuông tại A có 

\(\sin30^0=\dfrac{AB}{BC}\)

\(\Leftrightarrow BC=\dfrac{10\sqrt{3}}{3}:\dfrac{1}{2}=\dfrac{10\sqrt{3}}{3}\cdot2=\dfrac{20\sqrt{3}}{3}\left(cm\right)\)

a: Sửa đề: vẽ dây AD vuông góc với đường kính của (O) tại I

ΔABC vuông tại A

=>ΔABC nội tiếp đường tròn đường kính BC

=>BC là đường kính của (O)

mà AD vuông góc với đường kính của (O)

nên AD\(\perp\)BC tại I

=>B,I,C thẳng hàng

b: BC=2*OB=8cm

ΔABC vuông tại A

=>\(\widehat{ABC}+\widehat{ACB}=90^0\)

=>\(\widehat{ACB}=90^0-50^0=40^0\)

Xét ΔABC vuông tại A có \(sinACB=\dfrac{AB}{BC}\)

=>\(\dfrac{AB}{8}=sin40\)

=>\(AB\simeq5,14\left(cm\right)\)

ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(AC=\sqrt{8^2-5.14^2}\simeq6,13\left(cm\right)\)

c: ΔOAD cân tại O

mà OI là đường cao

nên I là trung điểm của AD

ΔABC vuông tại A có AI là đường cao

nên \(AI^2=IB\cdot IC\)

=>\(IB\cdot IC=IA\cdot ID\)