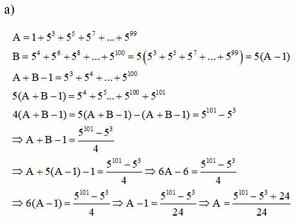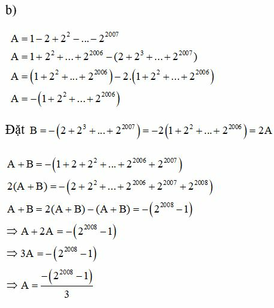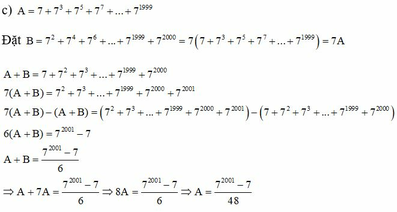A=(7+73)+(75+77)+....+(71997+71999)

A=7.(1+72)+75.(1+72)+....+71997.(1+72)

A=7.50+75.50+79.50+.....+71997.50

=>A chia hết cho 5 (1)

A=(7+73+75+....+71999)=7.(70+72+74+....+71998)

=>A chia hết cho 7 (2)

Mà ƯCLN(5;7)=1=>A chia hết cho 35

Ban kia lam dung roi

Lời giải:

Hiển nhiên $A\vdots 7$ do các số hạng đều chia hết cho 7.

Lại có:

$A=(7+7^3)+(7^5+7^7)+....+(7^{1997}+7^{1999})$

$=7(1+7^2)+7^5(1+7^2)+...+7^{1997}(1+7^2)$
$=(1+7^2)(7+7^5+...+7^{1997})$
$=50(7+7^5+...+7^{1997})\vdots 5$

Vậy $A\vdots 7, A\vdots 5$. Mà $(7,5)=1$

$\Rightarrow A\vdots 35$

a,  A = 1 + 5 3 + 5 5 + 5 7 + . . . + 5 99

B = 5 4 + 5 6 + 5 8 + . . . + 5 100 =  5 . ( 5 3 + 5 5 + 5 7 + . . . + 5 99 ) = 5(A – 1)

A + B – 1 =  5 3 + 5 4 + . . . + 5 100

5(A + B – 1) =  5 4 + 5 5 + . . . + 5 100 + 5 101

4(A + B – 1) = 5(A + B – 1) – (A + B – 1) =  5 101 - 5 3

=> A + B – 1 =  5 101 - 5 3 4

=> A + 5(A – 1) –1 =  5 101 - 5 3 4 => 6A – 6 =  5 101 - 5 3 4

=> A – 1 =  5 101 - 5 3 24

=> A =  5 101 - 5 3 + 24 24

b,  A = 1 - 2 + 2 2 - . . . - 2 2007

A = 1 + 2 2 + . . . + 2 2006 - 2 + 2 3 + . . . + 2 2007

A = ( 1 + 2 2 + . . . + 2 2006 ) - 2 . 1 + 2 2 + . . . + 2 2006

A = - 1 + 2 2 + . . . + 2 2006

Đặt  B = - 2 + 2 3 + . . . + 2 2007 =  - 2 . 1 + 2 2 + . . . + 2 2006 = 2A

A + B =  - 1 + 2 + 2 2 + . . . + 2 2006 + 2 2007

2(A+B) =  - 2 + 2 2 + . . . + 2 2006 + 2 2007 + 2 2008

A+B = 2(A+B)–(A+B) =  - 2 2008 - 1

=> A+2A =  - 2 2008 - 1

=> 3A =  - 2 2008 - 1

=> A =  - ( 2 2008 - 1 ) 3

c,  A = 7 + 7 3 + 7 5 + 7 7 + . . . + 7 1999

Đặt B =  7 2 + 7 4 + 7 6 + . . . + 7 1999 + 7 2000 =  7 ( 7 + 7 3 + 7 5 + 7 7 + . . . + 7 1999 ) = 7A

A+B =  7 + 7 2 + 7 3 + . . . + 7 1999 + 7 2000

7(A+B) =  7 2 + 7 3 + . . . + 7 1999 + 7 2000 + 7 2001

7(A+B) – (A+B) =  ( 7 2 + 7 3 + . . . + 7 1999 + 7 2000 + 7 2001 )  –  ( 7 + 7 2 + 7 3 + . . . + 7 1999 + 7 2000 )

6(A+B) =  7 2001 - 7

A+B =  7 2001 - 7 6

=> A + 7A =  7 2001 - 7 6 => 8A =  7 2001 - 7 6 => A =  7 2001 - 7 48

Xem lại đề không rõ qui luật

\(A=7+7^2+7^3+7^4+7^5+7^6+7^7+7^8\)

\(A=\left(7+7^3\right)+\left(7^2+7^4\right)+\left(7^5+7^7\right)+\left(7^6+7^8\right)\)

\(A=7\cdot\left(7+7^2\right)+7^2\cdot\left(1+7^2\right)+7^5\cdot\left(1+7^2\right)+7^6\cdot\left(1+7^2\right)\)

\(A=7\cdot50+7^2\cdot50+7^5\cdot50+7^6\cdot50\)

\(A=50\cdot\left(7+7^2+7^5+7^6\right)\)

\(A=5\cdot10\cdot\left(7+7^2+7^5+7^6\right)\)

Ta có: 5 ⋮ 5

⇒ \(A=5\cdot10\cdot\left(7+7^2+7^5+7^6\right)\) ⋮ 5 (đpcm) 

A = 7 + 72 + 73 + 74 + 75 + 76 + 77 + 78

A =  (7 + 73) + (72+ 74) + (75 + 77) + (76 + 78)

A = 7.(1 + 72)  + 72.(1 + 72) + 75.(1 + 72) + 76.(1 + 72)

A = 7.( 1 + 49) + 72.( 1 + 49) + 75.(1 + 49) + 76. (1 + 49)

A = 7.50 + 72.50 + 75.40 + 76.50

A = 50.(7 + 72 + 75 + 76)

Vì 50 ⋮ 5 nên A = 50.(7 + 72 + 76) ⋮ 5 đpcm

A = 7 + 7² + 7³ + 7⁴ + 7⁵ + 7⁶ + 7⁷ + 7⁸

A =  (7 + 7³) + (7²+ 7⁴) + (7⁵ + 7⁷) + (7⁶ + 7⁸)

A = 7.(1 + 7²)  + 7².(1 + 7²) + 7⁵.(1 + 7²) + 7⁶.(1 + 7²)

A = 7.( 1 + 49) + 7².( 1 + 49) + 7⁵.(1 + 49) + 7⁶. (1 + 49)

A = 7.50 + 7².50 + 7⁵.50 + 7⁶.50

A = 50.(7 + 7² + 7⁵ + 7⁶)

Vì 50 ⋮ 5 nên A = 50.(7 + 7² + 7⁶) ⋮ 5 đpcm

\(A=7\left(1+7+7^2\right)+7^4\left(1+7+7^2\right)+...+7^{118}\left(1+7+7^2\right)=7.57+7^4.57+...+7^{118}.57=57\left(7+7^4+...+7^{118}\right)⋮57\)

Lời giải:
$A=(7+7^2+7^3)+(7^4+7^5+7^6)+....+(7^{118}+7^{119}+7^{120})$
$=7(1+7+7^2)+7^4(1+7+7^2)+...+7^{118}(1+7+7^2)$

$=7.57+7^4.57+...+7^{118}.57$

$=57(7+7^4+...+7^{118})\vdots 57$ 

Ta có đpcm.

giúp mình với mình chuẩn bị phải nộp bài rồi T~T 

\(B=2+2^2+2^3+...+2^{60}\)

\(=2\left(1+2+2^2\right)+...+2^{58}\left(1+2+2^2\right)\)

\(=7\cdot\left(2+...+2^{58}\right)⋮7\)

Ta có :

A = 7 + 7³ + 7⁵ + 7⁷ + ... + 7¹⁹⁹⁷ + 7¹⁹⁹⁹

   = (7 + 7³) + (7⁵ + 7⁷) + ... + (7¹⁹⁹⁷ + 7¹⁹⁹⁹)

   = 7 (1 + 7²) + 7⁵ (1 + 7²) + ... + 7¹⁹⁹⁷ (1 + 7²)

   = 7 . 50 + 7⁵ . 50 + ... + 7¹⁹⁹⁷ . 50

   = 350 + 7⁴ . 350 + ... + 7¹⁹⁹⁶ . 350

   = 35 . 10 + 7⁴ . 35 . 10 + ... + 7¹⁹⁹⁶ . 35 . 10

   = 35 (10 + 7⁴ . 10 + ... + 7¹⁹⁹⁶ . 10) chia hết cho 35

Vậy A chia hết cho 35 (ĐPCM).

Đáp án của tôi cũng giống như bạn Trần Hùng Minh vậy .

A = 7+7^3+...+7^1999

A = 7.(1+49)+...+7^1997.(1+49)

A = 7.50+...+7^1997.50

A = 350+...+7^1996.7.50

A = 350+...+7^1996.350

A = 350.(1+...+7^1996) = 35.10.(1+...+7^1996) => A chia hết cho 35