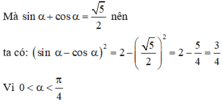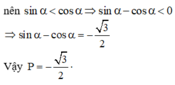Cho góc α thỏa mãn và sinα + cosα 0. Tính P sin3 α + cos3 α.
Đọc tiếp
Cho góc α thỏa mãn 
và sinα + cosα > 0. Tính P = sin3 α + cos3 α.
Những câu hỏi liên quan
Cho góc α thỏa mãn
0
α
π
4
và
sin
α
+
cos
α
5
2
. Tính P sinα - cosα 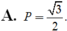A.
P
3
2
B. P 1 C. P -1/2 D.
P
-...
Đọc tiếp
Cho góc α thỏa mãn 0 < α < π 4 và sin α + cos α = 5 2 . Tính P = sinα - cosα
A.
P
=
3
2
B. P = 1
C. P = -1/2
D. P = - 3 2
Chọn D.
Ta có ( sinα - cosα) 2 + (sinα + cosα) 2 = 2( sin2α + cos2α) = 2.
Suy ra (sinα - cosα) 2 = 2 - ( sinα + cos α) 2 = 2 - 5/4 = 3/4.
Do 
suy ra sinα < cosα nên sinα - cosα < 0.
Vậy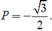 
Đúng 0
Bình luận (0)
Cho góc α thỏa mãn
sin
α
12
13
và
π
2
α
π
.Tính cosα.
Đọc tiếp
Cho góc α thỏa mãn sin α = 12 13 và π 2 < α < π .Tính cosα.
Cho góc α thỏa mãn tanα 2 và 1800 α 2700 . Tính P cosα + sinα
Đọc tiếp
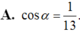
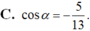
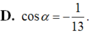
Cho góc α thỏa mãn tanα = 2 và 1800< α< 2700 . Tính P = cosα + sinα
Cho góc α thỏa mãn
π
2
α
2
π
và
tan
a
+
π
4
1
.Tính .
P
cos
α
-
π
6
+
sin
α
Đọc tiếp
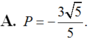
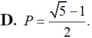
Cho góc α thỏa mãn π 2 < α < 2 π và tan a + π 4 = 1 .Tính . P = cos α - π 6 + sin α
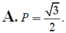
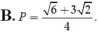
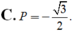
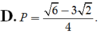
Cho góc α thỏa mãn sin2α = -4 / 5 và 3π / 4 < α < π. Tính P = sinα - cosα.
3/4pi<a<pi
=>sin a>0; cosa<0
sin2a=-4/5
=>2*sina*cosa=-4/5
=>sina*cosa=-2/5
(sina-cosa)^2=sin^2a+cos^2a-2*sina*cosa=1+4/5=9/5
=>sin a-cosa=3/căn 5
Đúng 0
Bình luận (0)
Cho góc α thỏa mãn
π
2
a
2
π
và
c
o
t
α
+
π
3
-
3
Tính giá trị của biểu thức
P
sin
α
+
π
6...
Đọc tiếp
Cho góc α thỏa mãn π 2 < a < 2 π và c o t α + π 3 = - 3 Tính giá trị của biểu thức P = sin α + π 6 + c o s α
A. P = 3 2
B. P = 1
C. P = -1
D. P = - 3 2
.Cho
α
là góc thỏa mãn
sin
α
1
4
.Tính giá trị của biểu thức
A
(
sin
4
α
+
2
sin
2
α
)
cos
α
A.
255
128
B.
225
182
C....
Đọc tiếp
Cho α là góc thỏa mãn sin α = 1 4 .Tính giá trị của biểu thức A = ( sin 4 α + 2 sin 2 α ) cos α
A. 255 128
B. 225 182
C. 255 182
D. 225 128
Cho góc
α
thỏa mãn:
π
2
α
π
và
sin
α
+
π
.Tính
tan
7
π
3
-
α
A.
3...
Đọc tiếp
Cho góc α thỏa mãn: π 2 < α < π và sin α + π .Tính tan 7 π 3 - α
A. 3 2
B. - 2
C. - 2 2
D. 4 2
Cho góc α thỏa mãn
0
α
π
4
v
à
sin
α
+
cos
α
5
2
. Giá trị của biểu thức P sin α - cosα là: A.
P
3
2
B.
P
1
2
C.
P...
Đọc tiếp
Cho góc α thỏa mãn 0 < α < π 4 v à sin α + cos α = 5 2 . Giá trị của biểu thức P = sin α - cosα là:
A. P = 3 2
B. P = 1 2
C. P = - 1 2
D. P = - 3 2
Chọn D.
Xét biểu thức (sin α - cosα ) 2 + (sin α + cosα ) 2 ta có:
(sin α - cosα ) 2 + (sin α + cosα ) 2
= sin 2 α - 2sin α.cosα + cos 2 α + sin 2 α + 2 sin α.cosα + cos 2 α
= 2( sin 2 α + cos 2 α ) =2
⇒ (sin α - cosα ) 2 = 2 - (sin α + cosα ) 2
Đúng 0
Bình luận (0)