Cho hàm số y -4x3 + 4x. Để y’ ≥ 0 thì x nhận các giá trị thuộc tập nào sau đây
Đọc tiếp
Cho hàm số y = -4x3 + 4x. Để y’ ≥ 0 thì x nhận các giá trị thuộc tập nào sau đây
Những câu hỏi liên quan
Cho hàm số
y
-
4
x
3
+
4
x
. Để
y
≥
0
thì x nhận các giá trị thuộc tập nào sau đây ? A.
-
3
;
3
B.
-
1
3
;...
Đọc tiếp
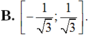
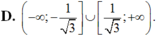
Cho hàm số y = - 4 x 3 + 4 x . Để y ' ≥ 0 thì x nhận các giá trị thuộc tập nào sau đây ?
A. - 3 ; 3
B. - 1 3 ; 1 3
C. ( - ∞ ; - 3 ] ∪ [ 3 ; + ∞ )
D. ( - ∞ ; - 1 3 ] ∪ [ 1 3 ; + ∞ )
Chọn B
Ta có
y = - 4 x 3 + 4 x ⇒ y ' = - 12 x 2 + 4
nên
y ' ≥ 0 ⇔ − 12 x 2 + 4 ≥ 0 ⇔ x 2 ≤ 1 3 ⇔ x ∈ − 1 3 ; 1 3
Đúng 0
Bình luận (0)
Cho hàm số . Để y’ 0 thì x nhận các giá trị thuộc tập nào sau đây? A. (-∞; +∞). D. ∅.
Đọc tiếp
Cho hàm số 
. Để y’ > 0 thì x nhận các giá trị thuộc tập nào sau đây?
A. (-∞; +∞).
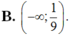
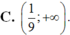
D. ∅.
Cho hàm số . Để y’ ≤ 0 thì x nhận các giá trị thuộc tập nào sau đây? A. ∅. B. (-∞; 0). C. (0; +∞). D. (-∞; 0].
Đọc tiếp
Cho hàm số 
. Để y’ ≤ 0 thì x nhận các giá trị thuộc tập nào sau đây?
A. ∅.
B. (-∞; 0).
C. (0; +∞).
D. (-∞; 0].
Cho hàm số y (2x2 + 1)3. Để y’ ≥ 0 thì x nhận các giá trị thuộc tập nào sau đây? A. ∅. B. (-∞; 0]. C. [0; +∞). D. R
Đọc tiếp
Cho hàm số y = (2x2 + 1)3. Để y’ ≥ 0 thì x nhận các giá trị thuộc tập nào sau đây?
A. ∅.
B. (-∞; 0].
C. [0; +∞).
D. R
Chọn C.
Ta có: y = (2x2 + 1)3 ⇒ y’ = 12x(2x2 + 1)2 ⇒ y’ ≥ 0 ⇔ x ≥ 0.
Đúng 0
Bình luận (0)
22 tháng 1 2022 lúc 21:32
cho hàm số y bằng -3x a, những điểm nào sau đây thuộc đồ thị của hàm số y bằng -3x b, tìm các giá trị của x để y nhận các giá trị dương
b: Để y dương thì -3x>0
hay x<0
Đúng 0
Bình luận (0)
Trong tất cả các cặp số (x,y) thỏa mãn
log
x
2
+
y
2
+
3
2
x
+
2
y
+
5
≥
1
, giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho...
Đọc tiếp
Trong tất cả các cặp số (x,y) thỏa mãn log x 2 + y 2 + 3 2 x + 2 y + 5 ≥ 1 , giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho x 2 + y 2 + 4 x + 6 y + 13 - m = 0 thuộc tập nào sau đây?
A. [8;10]
B. [5;7]
C. [1;4]
D. [-3;0]
Đáp án A
Ta có, giả thiết log x 2 + y 2 + 3 2 x + 2 y + 5 ≥ x 2 + y 2 + 3 ≤ 2 x + 2 y + 5 ⇔ x - 1 2 + y - 1 2 ≤ 4 là miền trong đường tròn tâm I(1;1) bán kính R 1 = 2
Và x 2 + y 2 + 4 x + 6 y + 13 - m = 0 ⇔ x + 2 2 + y + 3 2 = m là đường tròn tâm I(-2;-3); R 2 = m
Khi đó, yêu cầu bài toán ⇔ R 1 + R 2 = I 1 I 2 ⇔ m + 2 = 5 ⇔ m = 9
Đúng 0
Bình luận (0)
Trong tất cả các cặp số (x,y) thỏa mãn
log
x
2
+
y
2
+
3
(
2
x
+
2
y
+
5
)
≥
1
giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho x2 + y2 + 4x + 6y + 13 - m 0 thuộc tập nào sau đây?
Đọc tiếp
Trong tất cả các cặp số (x,y) thỏa mãn log x 2 + y 2 + 3 ( 2 x + 2 y + 5 ) ≥ 1 giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho x2 + y2 + 4x + 6y + 13 - m = 0 thuộc tập nào sau đây?
Đáp án A
Ta có, giả thiết
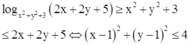
là miền trong đường tròn tâm I(1;1) bán kính R1 = 2
Và
Đúng 0
Bình luận (0)
Hãy vẽ đồ thị của các hàm số y 2x2, y -2x2. Dựa vào đồ thị để trả lời các câu hỏi sau:Nếu a 0 thì hàm số y ax2 đồng biến khi nào? Nghịch biến khi nào?Với giá trị nào của x thì hàm số đạt giá trị nhỏ nhất? Có giá trị nào của x để hàm số đạt giá trị lớn nhất không?Nếu a 0 thì hàm số đồng biến khi nào? Nghịch biến khi nào? Với giá trị nào của x thì hàm số đạt giá trị lớn nhất? Có giá trị nào của x để hàm số đạt giá trị nhỏ nhất không?
Đọc tiếp
Hãy vẽ đồ thị của các hàm số y = 2x2, y = -2x2. Dựa vào đồ thị để trả lời các câu hỏi sau:
Nếu a > 0 thì hàm số y = ax2 đồng biến khi nào? Nghịch biến khi nào?
Với giá trị nào của x thì hàm số đạt giá trị nhỏ nhất? Có giá trị nào của x để hàm số đạt giá trị lớn nhất không?
Nếu a < 0 thì hàm số đồng biến khi nào? Nghịch biến khi nào? Với giá trị nào của x thì hàm số đạt giá trị lớn nhất? Có giá trị nào của x để hàm số đạt giá trị nhỏ nhất không?
Vẽ hình:
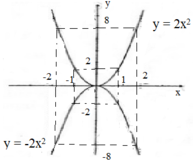
Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
Đúng 0
Bình luận (0)
Hãy vẽ đồ thị của các hàm số
y
2
x
2
,
y
-
2
x
2
. Dựa vào đồ thị để trả lời các câu hỏi sau:a) Nếu a 0 thì hàm số
y
a
x
2
đồng biến khi nào? Nghịch biến khi nào?Với giá trị nào của x thì hàm số đạt giá trị nhỏ nhất...
Đọc tiếp
Hãy vẽ đồ thị của các hàm số y = 2 x 2 , y = - 2 x 2 . Dựa vào đồ thị để trả lời các câu hỏi sau:
a) Nếu a > 0 thì hàm số y = a x 2 đồng biến khi nào? Nghịch biến khi nào?
Với giá trị nào của x thì hàm số đạt giá trị nhỏ nhất? Có giá trị nào của x để hàm số đạt giá trị lớn nhất không?
Nếu a < 0 thì hàm số đồng biến khi nào? Nghịch biến khi nào? Với giá trị nào của x thì hàm số đạt giá trị lớn nhất? Có giá trị nào của x để hàm số đạt giá trị nhỏ nhất không?
b) Đồ thị của hàm số y = a x 2 có những đặc điểm gì (trường hợp a > 0 , trường hợp a < 0)
Vẽ hình:
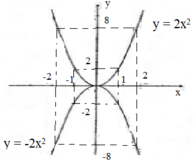
a) Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
b) Đồ thị hàm số y = a x 2 là đường cong (đặt tên là parabol) đi qua gốc tọa độ nhận trục tung Oy làm trục đối xứng.
Nếu a > 0 thì đồ thị nằm trên trục hoành, điểm O là điểm thấp nhất đồ thị (gọi là đỉnh parabol).
Nếu a < 0 thì đồ thị nằm bên dưới trục hoành, điểm O là điểm cao nhất của đồ thị.
Đúng 0
Bình luận (0)