Tính diện tích giới hạn bởi các đường cong y = (x - 1)lnx và y = x - 1.
A. e 2 - 4 e + 5 4
B. 3 e 2 - 2 e + 5 2
C. 7 e 2 - e + 2 3
D. 4 e 2 + 3 e - 2 5
Cho hình thang cong (H) giới hạn bởi các đường y = ln x + 1 , trục hoành và đường thẳng x = e − 1. Tính thể tích khối tròn xoay thu được khi quay hình H quanh trục Ox .
A. e − 2.
B. 2 π
C. π . e .
D. π . e − 2 .
Tính diện tích giới hạn bởi các đường cong y=(e+1)x; y = (ex + 1)x
A. e 5 - 19 100
B. 2 e 3 - 73 50
C. e 3 - 11 20
D. e 2 - 1
Chọn D.
Hoành độ giao điểm của hai đường là nghiệm của phương trình (e+1)x = ( 1 + e x ) x <=> x = 0 hoặc x =1
Diện tích cần tính là S = ∫ 0 1 x e x d x - ∫ 0 1 e x d x = ∫ 0 1 x d ( e x ) - e ∫ 0 1 x d x
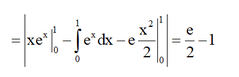
Diện tích hình phẳng được giới hạn bởi các đường y = ln x , x = 1 e , x = e và trục hoành là
A. 1 - 1 e
B. 2 1 + 1 e
C. 2 1 - 1 e
D. 1 + 1 e
Tính thể tích của vật thể tròn xoay tạo bởi khi quay quanh trục hoành Ox hình phẳng giới hạn bởi các đường thẳng y = lnx , y = 0 , x = 1 , x = e .
A. e - 2
B. e + 2
C. π e + 2 .
D. π ( e − 2 ) .
Tính thể tích của vật thể tròn xoay tạo bởi khi quay quanh trục hoành Ox hình phẳng giới hạn bởi các đường thẳng y = ln x ; y = 0 ; x = 1 ; x = e
A. e - 2
B. e + 2
C. π ( e + 2 )
D. π ( e - 2 )
Tính diện tích hình phẳng giới hạn bởi các đường:
a) y = X2, y = x + 2; b) y = |lnx|, y = 1; c) y = (x – 6)2, y = 6x– x2
a) Phương trình hoành độ giao điểm f(x) = X2 - x - 2 =0 ⇔ x = -1 hoặc x = 2.
Diện tích hình phẳng cần tìm là :
b) Phương trình hoành độ giao điểm:
f(x) = 1 - ln|x| = 0 ⇔ lnx = ± 1
⇔ x = e hoặc
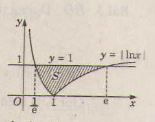
y = ln|x| = lnx nếu lnx ≥ 0 tức là x ≥ 1.
hoặc y = ln|x| = - lnx nếu x < 0, tức là 0 < x < 1.
Dựa vào đồ thị hàm số vẽ ở hình trên ta có diện tích cần tìm là :
Ta có ∫lnxdx = xlnx - ∫dx = xlnx – x + C, thay vào trên ta được :
c) Phương trình hoành độ giao điểm là:
f(x) = 6x – x2 – (x - 6)2 = -2(x2 – 9x +18)
f(x) = 0 ⇔ -2(x2 – 9x +18) ⇔ x = 3 hoặc x = 6.
Diện tích cần tìm là:
Tính diện tích hình phẳng giới hạn bởi các đường:
a) y = X2, y = x + 2; b) y = |lnx|, y = 1; c) y = (x – 6)2, y = 6x– x2
a) Phương trình hoành độ giao điểm f(x) = X2 - x - 2 =0 ⇔ x = -1 hoặc x = 2.
Diện tích hình phẳng cần tìm là :
b) Phương trình hoành độ giao điểm:
f(x) = 1 - ln|x| = 0 ⇔ lnx = ± 1
⇔ x = e hoặc

y = ln|x| = lnx nếu lnx ≥ 0 tức là x ≥ 1.
hoặc y = ln|x| = - lnx nếu x < 0, tức là 0 < x < 1.
Dựa vào đồ thị hàm số vẽ ở hình trên ta có diện tích cần tìm là :
Ta có ∫lnxdx = xlnx - ∫dx = xlnx – x + C, thay vào trên ta được :
c) Phương trình hoành độ giao điểm là:
f(x) = 6x – x2 – (x - 6)2 = -2(x2 – 9x +18)
Hình phẳng giới hạn bởi các đường cong y = x ( 1 - x ) và y = x 3 - x có diện tích bằng
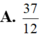
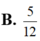
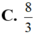
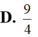
Hình phẳng giới hạn bởi các đường cong y = x ( 1 - x ) và y = x 3 - x có diện tích bằng
A . 37 12
B . 5 12
C . 8 3
D . 9 4