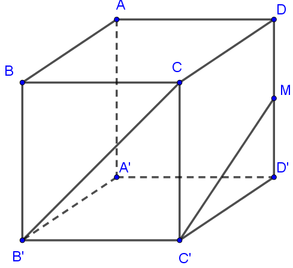
Cho hình lập phương ABCD.A’B’C’D’. Gọi M là trung điểm của DD’ (tham khảo hình vẽ dưới đây). Tính cosin của góc giữa hai đường thẳng B’C và C’M.
A. 1 3
B. 1 10
C. 1 3
D. 2 2 9
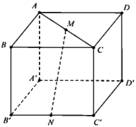
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N lần lượt là trung điểm của AC và B’C’ (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng MN và B’D’ bằng
A. 5 a
B. 5 a 5 .
C. 3a
D. a 3 .
Đáp án D.
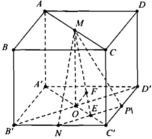
Gọi P là trung điểm của C’D’ suy ra d = d O ; M N P
Dựng:
O A ⊥ N P ; OF ⊥ ME ⇒ d=OF= M O . N E M O 2 + N E 2
trong đó
M O = a ; N E = a 2 4 ⇒ d = a 3 .
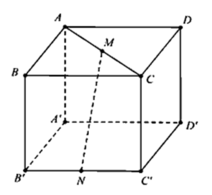
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N lần lượt là trung điểm của AC và B’C’ (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng MN và B’D’ bằng
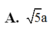
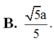
![]()
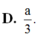
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N lần lượt là trung điểm của AC và B’C’ (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng MN và B’D’ bằng

A. 5 a
B. 5 a 5
C. 3a
D. a/3
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N lần lượt là trung điểm của AC và B’C’ (tham khảo hình vẽ bên).
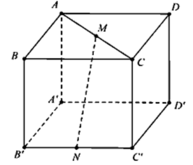
Khoảng cách giữa hai đường thẳng MN và B’D’ bằng
A. 5 a
B. 5 a 5
C. 3a.
D. a 3
Cho hình lập phương ABCD.A’B’C’D’. Gọi M là trung điểm CD. Cosin của góc giữa AC và C’M là:
A. 0.
B. 2 2 .
C. 1 2 .
D. 10 10 .
Cho hình lập phương ABCD.A’B’C’D’. Gọi M là trung điểm CD. Cosin của góc giữa AC và C’M là:
B. 2 2 .
C. 1 2 .
D. 10 10 .
Đáp án D
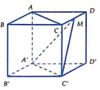
Giả sử hình lập phương có cạnh là 1.
A ' C // A C ⇒ A C , C ' M ^ = A ' C ' , C ' M ^
Xét Δ A ' C ' M ' có:
A ' C ' = 2 , C ' M = 1 2 + 1 2 2 = 5 2 , A ' M = A ' D 2 + M D 2 = 2 + 1 4 = 3 2
Định lí Cô sin: a 2 = b 2 + c 2 − 2 b c cos A ⇒ cos A = b 2 + c 2 − a 2 2 b c ta được: cos A C , C ' M ^ = 1 10 .
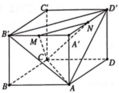
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 2. Gọi M,N lần lượt là trung điểm các cạnh A’B’ và A’D’(tham khảo hình vẽ). Cosin của góc tạo bởi hai mặt phẳng (CMN) và (AB’D’) bằng
A. 3 51 102
B. 51 102
C. 2 51 51
D. 51 51
Cho hình lập phương ABCD.A’B’C’D’. Gọi M,N,P lần lượt là trung điểm của các cạnh AB, AD, C’D’. Tính cosin góc giữa hai đường thẳng MN và CP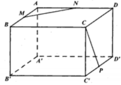
![]()
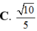
![]()
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng 1. Gọi K là trung điểm của DD′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng CK và A′D bằng
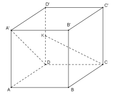
A. 10 5
B. 4 5
C. 10 10
D. 2 5