Cho hàm số y = a x 3 + bx 2 + c x + d có bảng biến thiên:
Cho các mệnh đề:
(1) Hệ số b < 0
(2) Hàm số có y CD = 2 ; y CT = - 2
(3) y''(0) < 0
(4) Hệ số c = 0, d = 1
Có bao nhiêu mệnh đề đúng:
A. 1
B. 2
C. 3
D. 4
Cho hàm số
y
=
ax
+
b
x
+
c
có bảng biến thiên dưới đây:\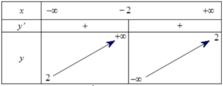
Cho các mệnh đề:
(1) Hàm số đồng biến trên toàn tập xác định.
(2) Hệ số a = 2, c = 2
(3) Nếu y ' = 3 x + 2 2 thì b = 1
(4) Đồ thị hàm số nhận giao của 2 đường tiệm cận I(-2;2) là tâm đối xứng.
Có bao nhiêu mệnh đề sai?
A. 4
B. 3
C. 1
D. 0
Cho hàm số y = x 3 − 6 x 2 + 9 x − 1 và các mệnh đề sau:
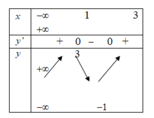
(1) Hàm số đồng biến trên các khoảng − ∞ ; 1 và 3 ; + ∞
nghịch biến trên khoảng (1;3)
(2) Hàm số đạt cực đại tại x = 3và x = 1
(3) Hàm số có y C D + 3 y C T = 0
(4) Hàm số có bảng biến thiên và đồ thị như hình vẽ.
Tìm số mệnh đề đúng trong các mệnh đề trên.
A. 1
B. 4
C. 2
D. 3
Đáp án D
Phương pháp: +) Khảo sát sự biến thiên của đồ thị hàm số.
+) Hàm số đạt cực trị tại điểm x = x 0 ⇔ y ' x 0 = 0 và x = x 0 được gọi là điểm cực trị.
+) Hàm số đạt cực trị tại điểm x = x 0 thì y x 0 là giá trị cực trị.

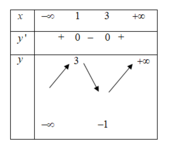

Như vậy có 3 mệnh đề đúng.
Chú ý: Học sinh thường giá trị cực trị và
điểm cực trị nên có thể chọn sai mệnh dề (2) đúng.
Cho hàm số có bảng biến thiên:
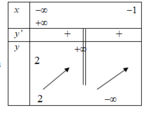
Xét các mệnh đề:
(1) c = 1
(2) c = 2
(3) Hàm số đồng biến trên − ∞ ; − 1 ∪ − 1 ; + ∞
(4) Nếu thì y ' = 1 x + 1 2
Tìm số mệnh đề đúng trong các mệnh đề trên.
A. 3
B. 4
C. 1
D. 2
Đáp án A
Phương pháp: Dựa vào BBT để kết luận tính đơn điệu của hàm số và suy ra các giá trị a, c tương ứng.
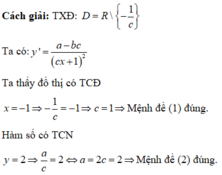
Theo BBT ta thấy hàm số đồng biến trên từng khoảng xác định của hàm số.
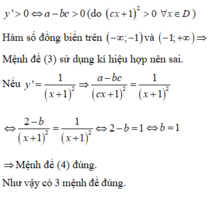
Câu 48. Cho y=|x+1|+|x−2|và các mệnh đề
1)Hàm số tăng lên trên(-1,+∞)
2)Hàm số không đổi trên[−1;2)
3) Hàm số giảm trên(-∞,-1)
4) Hàm số giảm trên (-2,+∞)
Hỏi có bao nhiêu mệnh đề đúng?
A. 0 B. 1 C. 2 D. 3
Câu 49. Hàm số y=-√|2x+3|nghịch biến trên khoảng.
A.(\(-\dfrac{3}{2},+\infty\))
B.(-∞,\(-\dfrac{3}{2}\))
C. R
D.Cả 3 đáp án đều sai
Cho hàm số y = f(x) có bảng biến thiên như hình dưới đây
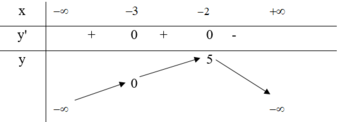
I. Hàm số đồng biến trên khoảng - 3 ; - 2
II. Hàm số đồng biến trên khoảng - ∞ ; 5
III. Hàm số nghịch biến trên các khoản - 2 ; + ∞
IV. Hàm số đồng biến trên khoảng - ∞ ; - 2
Số mệnh đề sai trong các mệnh đề trên là
A. 2
B. 3
C. 4
D. 1
Đáp án D
Khẳng định số II sai.
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng - ∞ ; - 2
Cho hàm số y = f(x) có bảng biến thiên như hình dưới đây.
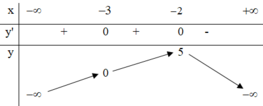
I. Hàm số đồng biến trên khoảng (-3;-2)
II. Hàm số đồng biến trên khoảng − ∞ ; 5 .
III. Hàm số nghịch biến trên các khoản − 2 ; + ∞ .
IV. Hàm số đồng biến trên khoảng − ∞ ; − 2 .
Số mệnh đề sai trong các mệnh đề trên là
A. 2
B. 3
C. 4
D. 1
Đáp án D
Khẳng định số II sai. Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng ( − ∞ ; − 2 )
Cho hàm số y=f(x) xác định, liên tục trên tập R\{1} và có bảng biến thiên
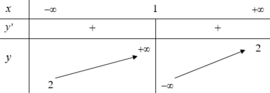
Số mệnh đề đúng trong các mệnh đề sau là?
1. Đường thẳng y=2 là đường tiệm cận ngang của đồ thị hàm số.
2. Đường thẳng x=1 là đường tiệm cận đứng của đồ thị hàm số.
3. Hàm số đồng biến trên các khoảng - ∞ ; 1 và 1 ; + ∞
A. 0.
B. 1
C. 2.
D. 3
Cho hàm số y=f(x) có bảng biến thiên như hình dưới đây.
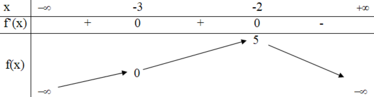
I. Hàm số đồng biến trên khoảng (-3;-2)
II. Hàm số đồng biến trên khoảng − ∞ ; 5 .
III. Hàm số nghịch biến trên khoảng − 2 ; + ∞ .
IV. Hàm số đồng biến trên khoảng - ∞ ; - 2
Số mệnh đề sai trong các mệnh đề trên là
A. 2.
B. 3.
C. 4.
D. 1.
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f' (x) như hình vẽ bên. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:

1. Hàm số g(x) có 3 điểm cực trị.
2. Hàm số g(x)đạt cực tiểu tại x = 0.
3. Hàm số g(x)đạt cực đại tại x = 2.
4. Hàm số g(x)đồng biến trên khoảng (-2;0).
5. Hàm số g(x)nghịch biến trên khoảng (-1;1).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 1.
B. 4.
C. 3.
D. 2.