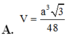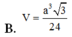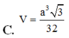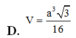Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 10. Gọi M là điểm trên SA sao cho S M S A = 2 3 . Một mặt phẳng (α) đi qua M song song với AB và CD, cắt hình chóp theo một tứ giác có diện tích là:
A. 400 9 .
B. 16 9 .
C. 4 9 .
D. 20 3 .
Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng 10. \(M\) là điểm trên \(SA\) sao cho \(\frac{{SM}}{{SA}} = \frac{2}{3}\). Một mặt phẳng \(\left( \alpha \right)\) đi qua \(M\) song song với \(AB\) và \(C{\rm{D}}\), cắt hình chóp theo một tứ giác có diện tích là
A. \(\frac{{400}}{9}\).
B. \(\frac{{200}}{3}\).
C. \(\frac{{40}}{9}\).
D. \(\frac{{200}}{9}\).
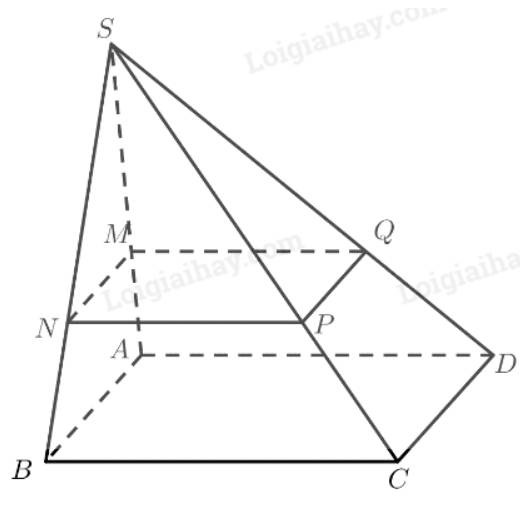
Qua \(M\) dựng đường thẳng song song với \(AB\), cắt \(SB\) tại \(N\).
Qua \(N\) dựng đường thẳng song song với \(BC\), cắt \(SC\) tại \(P\).
Qua \(M\) dựng đường thẳng song song với \(AD\), cắt \(SD\) tại \(Q\).
Ta có:
\(\left. \begin{array}{l}MN\parallel AB\\AB \subset \left( {ABCD} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {ABCD} \right)\)
\(\left. \begin{array}{l}MQ\parallel AD\\AD \subset \left( {ABCD} \right)\end{array} \right\} \Rightarrow MQ\parallel \left( {ABCD} \right)\)
\(\left. \begin{array}{l}MN\parallel \left( {ABCD} \right)\\MQ\parallel \left( {ABCD} \right)\\MN,MQ \subset \left( \alpha \right)\end{array} \right\} \Rightarrow \left( {MNPQ} \right)\parallel \left( {ABCD} \right)\)
\( \Rightarrow \frac{{{S_{MNPQ}}}}{{{S_{ABC{\rm{D}}}}}} = {\left( {\frac{{MN}}{{AB}}} \right)^2}\)
Ta có: \({S_{ABC{\rm{D}}}} = A{B^2} = {10^2} = 100\)
\(MN\parallel AB \Rightarrow \frac{{MN}}{{AB}} = \frac{{SM}}{{SA}} = \frac{2}{3}\)
\( \Rightarrow \frac{{{S_{MNPQ}}}}{{{S_{ABC{\rm{D}}}}}} = {\left( {\frac{2}{3}} \right)^2} = \frac{4}{9} \Rightarrow {S_{MNPQ}} = \frac{4}{9}{S_{ABC{\rm{D}}}} = \frac{4}{9}.100 = \frac{{400}}{9}\)
Chọn A.
cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. O là tâm đáy. Gọi M,N là trung điểm SA, BC.biết (MN,(ABCD))=60⁰ tính d(M,( SCD))
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. Gọi M và N lần lượt là trung điểm của SA và CD. Cho biết MN tạo với mặt đáy một góc bằng 30 0 . Tính thể tích khối chóp S.ABCD .
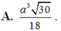
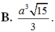
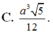
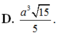
Cho hình chóp tứ giác đều S . A B C D có cạnh đáy bằng a. Gọi M và N lần lượt là trung điểm của SA và CD. Cho biết MN tạo với mặt đáy một góc bằng 30 o . Tính thể tích khối chóp S . A B C D .
A. a 3 30 18
B. a 3 15 3
C. a 3 5 12
D. a 3 15 5
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác đều, mặt bên SCD là tam giác vuông cân tại S. Gọi M là điểm thuộc đường thẳng CD sao cho BM vuông góc với SA. Thể tích khối chóp S.BDM bằng
A. a 3 3 48
B. a 3 3 24
C. a 3 3 32
D. a 3 3 16
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, tam giác SBD đều cạnh a. Gọi M, P là hai điểm lần lượt di động trên cạnh SA, SC (không trùng với S) sao cho SA/SM + SC/ SP = 3, (a) là mặt phẳng di động chứa M, P cắt SB, SD lần lượt tại N, Q. Diện tích tam giác SNQ đạt giá trị nhỏ nhất là
Bài này ứng dụng 1 phần cách giải của bài này:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giả sử mp (a) cắt SA; SB;SC; SD thứ tự tại A' B' C' D'. Tính \(\dfra... - Hoc24
Gọi O' là giao điểm của SO và MP, tương tự như bài trên, ta có 3 đường thẳng SO, MP, NQ đồng quy tại O'
Đồng thời sử dụng diện tích tam giác, ta cũng chứng minh được:
\(3=\dfrac{SA}{SM}+\dfrac{SC}{SP}=\dfrac{2SO}{SO'}=\dfrac{SB}{SN}+\dfrac{SD}{SQ}\)
Áp dụng BĐT Cô-si: \(3=\dfrac{SB}{SN}+\dfrac{SD}{SQ}\ge2\sqrt{\dfrac{SB.SD}{SN.SQ}}\Rightarrow SN.SQ\ge\dfrac{4}{9}.SB.SD\)
Theo bổ đề về diện tích tam giác chứng minh ở đầu:
\(\dfrac{S_{SNQ}}{S_{SBD}}=\dfrac{SN.SQ}{SB.SD}\ge\dfrac{\dfrac{4}{9}SB.SD}{SB.SD}=\dfrac{4}{9}\)
\(\Rightarrow S_{SBD}\ge\dfrac{4}{9}.S_{SBD}=\dfrac{4}{9}.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^2\sqrt{3}}{9}\)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a mặt bên SAB là tam giác đều, mặt bên SCD là tam giác vuông cân tại S, gọi M là điểm thuộc đường thẳng CD sao cho BM vuông góc với SA. Tính thể tích V của khối chóp S.BDM
A. V = a 3 3 48
B. V = a 3 3 24
C. V = a 3 3 32
D. V = a 3 3 16
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác đều, mặt bên SCD là tam giác vuông cân tại S. Gọi M là điểm thuộc đường thẳng CD sao cho BM vuống góc với SA. Tính thể tích V của khối chóp S.BDM?
A. V = a 3 3 16
B. V = a 3 3 24
C. V = a 3 3 32
D. V = a 3 3 48
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a mặt bên SAB là tam giác đều, mặt bên SCD là tam giác vuông cân tại S, gọi M là điểm thuộc đường thẳng CD sao cho BM vuông góc với SA. Tính thể tích V của khối chóp S.BDM