Cho véc tơ n → ≠ 0 → và hai véc tơ không cùng phương a → , b → . Nếu véc tơ n → vuông góc với a → , b → thì ba véc tơ n → , a → , b →
A. Đồng phẳng.
B. Có thể đồng phẳng.
C. Có thể không đồng phẳng.
D. Không đồng phẳng.
Trong không gian với hệ tọa độ Oxyz, cho véc-tơ ![]() =(1;0;-2). Trong các véc-tơ sau đây, véc-tơ nào không cùng phương với véc-tơ
=(1;0;-2). Trong các véc-tơ sau đây, véc-tơ nào không cùng phương với véc-tơ ![]() ?
?
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(0;-1;-2) và B(2;2;2). Véc-tơ ![]() nào dưới đây là một véc-tơ chỉ phương của đường thẳng AB?
nào dưới đây là một véc-tơ chỉ phương của đường thẳng AB?
A. ![]() =(2;1;0)
=(2;1;0)
B. ![]() =(2;3;4)
=(2;3;4)
C. ![]() =(-2;1;0)
=(-2;1;0)
D. ![]() =(2;3;0).
=(2;3;0).
Đáp án B
Ta có ![]() =(2;3;4). Suy ra véc-tơ
=(2;3;4). Suy ra véc-tơ ![]() =(2;3;4) là một véc-tơ chỉ phương của đường thẳng AB.
=(2;3;4) là một véc-tơ chỉ phương của đường thẳng AB.
Trong không gian Oxyz , cho đường thẳng d đi qua điểm M nhận véc tơ a ⇀ làm véc tơ chỉ phương và đường thẳng d ' đi qua điểm M ' nhận véc tơ a ' ⇀ làm véc tơ chỉ phương. Điều kiện để đường thẳng d trùng với đường thẳng d ' là
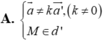
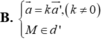
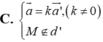
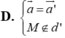
Trong không gian Oxyz , cho đường thẳng d đi qua điểm M nhận véc tơ a → làm véc tơ chỉ phương và đường thẳng d ' đi qua điểm M ' nhận véc tơ a ' → làm véc tơ chỉ phương. Điều kiện để đường thẳng d trùng với đường thẳng d ' là
A. a → ≠ k a ' → , k ≠ 0 M ∈ d '
B. a → = k a ' → , k ≠ 0 M ∈ d '
C. a → = k a ' → , k ≠ 0 M ∉ d '
D. a → = a ' → M ∉ d '
Đáp án B
Phương pháp:
Điều kiện để hai đường thẳng trùng nhau là hai véc tơ chỉ phương cùng phương và một điểm thuộc đường thẳng này cũng thuộc đường thẳng kia
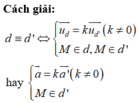
Câu 1: Không dùng hình vẽ,CMR với 5 điểm bất kì A,B,C,K,M ta có véc tơ MK + véc tơ AB + véc tơ BC + véc tơ CA= véc tơ MK Câu 2: Cho đoạn thẳng AB.O là trung điểm của AB CM: véc tơ OA + véc tơ OB= véc tơ 0 Làm hộ mik ạ,mik cảm ơn ạ
c1 ta có vector AB+vecAC+vecBC=vec0
c2ta co vector OA=-vector OB AOB thẳng hàng nhưng ngược chiều=>vector OA+vectorOB=vectorOA-vector OA=vec0
hojk tốt=>>>>>>>>>>>>>>>>>>>>>>>>>
Cho tam giác ABC có 3 trung tuyến AM,BN,CK và trọng tâm G. Chứng minh:
a/véc tơ AM + véc tơ BN + véc tơ CK = véc tơ 0 ( đã xong )
b/ véc tơ GM + véc tơ GN + véc tơ GK = véc tơ 0 ( đã xong )
c/ 3.véc tơ AG = 2.(véc tơ AK + véc tơ AN )
Làm giúp mình câu c thôi ạ :(
Theo tính chất trọng tâm ta có: \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\)
Mặt khác AM là trung tuyến nên: \(\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)\Rightarrow3\overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{AC}\) (1)
K là trung điểm AB, N là trung điểm AC nên: \(\left\{{}\begin{matrix}\overrightarrow{AK}=\dfrac{1}{2}\overrightarrow{AB}\\\overrightarrow{AN}=\dfrac{1}{2}\overrightarrow{AC}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=2\overrightarrow{AK}\\\overrightarrow{AC}=2\overrightarrow{AN}\end{matrix}\right.\) (2)
(1);(2) \(\Rightarrow3\overrightarrow{AG}=2\left(\overrightarrow{AK}+\overrightarrow{AN}\right)\)
Cho tứ giác ABCD.Gọi M,N là trung điểm của AD và BC ,O là điểm thuộc đoạn MN sao cho OM=2ON
a, cm: 2 véc tơ MN=véc tơ AB+véc tơ DC
b, cm:véc tơ OA -2 véc tơ OB-2véc tơ OC +OD=véc tơ 0
Mình không biết trả lời.Mình mới học lớp 5 thôi .Mong bạn thông cảm nhé!
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;1;0) và B(0;1;2). Véc-tơ nào dưới đây là một véc-tơ chỉ phương của đường thẳng AB?
![]()
![]()
![]()
![]()
Đáp án B
![]() là một véc-tơ chỉ phương của đường thẳng AB.
là một véc-tơ chỉ phương của đường thẳng AB.
Cho tứ giác lồi ABCD. Gọi M;N;P;Q lần lượt là trung điểm của AB; BC;CD;DA.Chứng minh rằng:
a) véc tơ MP=1/2.(véc tơ AD+ véc tơ BC)
b) Hai tam giác ANP và CMQ có cùng trọng tâm