Cho số thực m > 0. Điều kiện cần và đủ để hai tập hợp − ∞ ; 1 m và ( 4 m ; + ∞ ) có giao khác rỗng là:
A. 0 < m ≤ 1 2
B. 0 < m < 1 2
C. 0 < m < 1 4
D. 0 < m ≤ 1 4
Xét phương trình bậc hai az2+bz+c=0 trên tập C a ≠ 0 , a , b , c ∈ R . Tìm điều kiện cần và đủ để phương trình có hai nghiệm z1 và z2 là số phức liên hợp với nhau.
![]()
![]()
![]()
![]()
Cho số thực a < 0. Điều kiện cần và đủ để − ∞ ; 9 a ∩ 4 a ; + ∞ ≠ 0 là:
A. − 2 3 < a < 0
B. − 2 3 ≤ a < 0
C. − 3 4 < a < 0
D. − 3 4 ≤ a < 0
Cho số thực a < 0. Điều kiện cần và đủ để (-∞; 9a] ∩ [ 4 a ; +∞) ≠ ∅ là:
A. - 2 3 < a < 0
B. - 2 3 ≤ a < 0
C. - 3 4 < a < 0
D. - 2 3 ≤ a < 0
Đáp án: B
( - ∞ ; 9 a ) ∩ [ 4 a ; + ∞ ) ≠ ∅ ⇔ 9 a ≥ 4 a ⇔ 9 a 2 ≤ 4 ( d o a < 0 ) ⇔ a ≥ - 2 3 h o ặ c a ≥ 2 3 . M à a < 0 n ê n - 2 3 ≤ a < 0 .
Cho hàm số y = f(x) có đồ thị hàm số y = f ' x như hình vẽ:

Xét hàm số g x = 2 f x + 2 x 3 − 4 x − 3 m − 6 5 với m là số thực. Điều kiện cần và đủ để g x ≤ 0 ∀ x ∈ − 5 ; 5 là:
A. m ≥ 2 3 f 5
B. m ≥ 2 3 f − 5
C. m ≥ 2 3 f 0
D. m ≤ 2 3 f 5
Câu 4:Trong các mệnh đề sau, mệnh đề nào sai? A. Để tứ giác là hình bình hành, điều kiện cần và đủ là hai cạnh đối song song và bằng nhau. B. Để điều kiện đủ là . C. Để tổng của hai số nguyên chia hết cho 13, điều kiện cần và đủ là mỗi số đó chia hết cho 13. D. Để có ít nhất một trong hai số là số dương điều kiện đủ là .
Cho hàm số y=f(x). Đồ thị hàm số y=f'(x) như hình vẽ. Đặt g ( x ) = 3 f ( x ) - x 3 + 3 x - m , với m là tham số thực. Điều kiện cần và đủ để bất phương trình g x ≥ 0 nghiệm đúng với x ∈ - 3 ; 3 là
A. m ≤ 3 f 3
B. m ≤ 3 f 0
C. m ≥ 3 f 1
D. m ≥ 3 f - 3
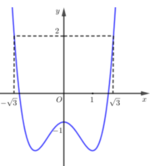
Tìm điều kiện cần và đủ về các số thực m,n để phương trình z 4 + m z 2 + n = 0 không có nghiệm thực
![]()
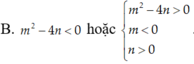
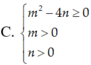

Cho số thực a<0.Tìm điều kiện cần và đủ để hai khoảng âm vô cùng đến 4a và khoảng 9/a đến duơng vô cùng có giao khác rỗng.
Cho hàm số y=f(x) có đạo hàm liên tục trên , đồ thị hàm số y=f’(x) như hình vẽ bên dưới. Cho bất phương trình f e x + 2 3 e 3 x - e x - m ≥ 0 ; với m là tham số thực. Tìm điều kiện cần và đủ để bất phương trình f e x + 2 3 e 3 x - e x - m ≥ 0 đúng với mọi x ∈ - 2 ; 2
A. m ≤ f e + 2 3 e 3 - e
B. m ≤ f 1 - 1 3
C. m ≤ f 1 e + 2 3 e - 3 - e - 1
D. m ≤ f e 2 + 2 3 e 3 2 - e 2