1.

Phương trình đường thẳng có dạng:

\(2\left(x-2\right)-1\left(y-1\right)=0\Leftrightarrow2x-y-3=0\)

2.

Do d song song \(\Delta\) nên nhận \(\left(2;-3\right)\) là 1 vtpt

Phương trình: \(2\left(x-1\right)-3\left(y-1\right)=0\Leftrightarrow2x-3y+1=0\)

3.

Do đường thẳng vuông góc d nên nhận \(\left(3;4\right)\) là 1vtpt

\(3\left(x-2\right)+4\left(y-3\right)=0\Leftrightarrow3x+4y-18=0\)

CHỌN C vì :

Hệ số góc của đường thẳng d có vectơ chỉ phương u→ = (-1; \(\sqrt{3}\)) là:

\(K=\dfrac{U_2}{U_1}=\dfrac{\sqrt{3}}{-1}=-\sqrt{3}\)

\(=>C.K=-\sqrt{3}\)

Hệ số góc của `\Delta` là: `k=[u_2]/[u_1]=\sqrt{3}/[-1]=-\sqrt{3}`

     `->\bb C`

a) Phương trình đường thẳng Δ đi qua M(–5; –8) và có hệ số góc k = –3 là:

y = –3.(x + 5) – 8 ⇔ 3x + y + 23 = 0.

b) Ta có: A(2; 1), B(–4; 5) ⇒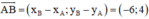 

Δ đi qua hai điểm A(2; 1) và B(–4; 5)

⇒ Δ nhận 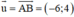 là một vtcp

⇒ Δ nhận 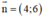 là một vtpt.

Phương trình tổng quát của đường thẳng Δ là:

(Δ) : 4(x – 2) + 6(y -1) = 0

Hay 4x + 6y – 14 = 0 ⇔ 2x + 3y – 7 = 0.

a.

Hai đường thẳng song song khi:

\(\dfrac{m+3}{2}=\dfrac{3}{2}\ne\dfrac{-2m+3}{2-3m}\)

\(\Leftrightarrow m=0\)

b.

Hai đường thẳng trùng nhau khi: \(\dfrac{m+3}{2}=\dfrac{3}{2}=\dfrac{-2m+3}{2-3m}\Rightarrow\) ko tồn tại m thỏa mãn

Vậy 2 đường thẳng cắt nhau khi \(m\ne0\)

Chọn D.

Phương trình tổng quát của đường thẳng Δ đi qua điểm M(-1;2) và có hệ số góc k = 3 là: y = 3(x + 1) + 2 ⇔ 3x - y + 5 = 0

Đáp án D

Ta có: y ' = 8 x + 2 2 ⇒ k 0 = y ' − 3 = 8.  

mỗi bài, mk làm một phần ví dụ cho cậu nhé

nó đối xứng với nhau qua pt đường thẳng đenta,

trường hợp (d) ko cắt (đen ta) hay (d) cắt (đen ta) thì đều làm theo phương pháp sau 

lấy 2 điểm bất kì thuộc (d) thì ta có như sau: A(0:1)  là điểm thuộc đường thẳng (d)

lấy A' đối xứng với A qua (đen ta) 

liên hệ tính chất đối xứng qua đường thẳng thì hiểu là AA' vuông góc (đen ta)

đồng thời giao điểm của  AA' với (đen ta) là trung điểm của  AA' 

dễ dàng tìm đc giao điểm của (đen ta) với (d) là K(-2/5;1/5)

từ pt (đenta) thì dễ dàng =) vecto pháp tuyến của (đenta) =) (3;-4) 

vì AA' vuông góc với (đenta) nên =) vectơ pháp tuyến của AA' là (4;-3)

áp véctơ pháp tuyến của AA' vào phương trình tổng quát đc: 4(x-0)-3(y-1)=0 (=) 4x-3y+3=0

gọi I là giao điểm của AA' và (đenta) =) I(-6/7;-1/7)

mà I là trung điểm của AA' 

chắc chắn cậu sẽ dễ dàng suy ra điểm A'

mà K và A' thuộc (d') nên dễ dàng =) phương trình của (d')