Cho bất phương trình: (2m + 1)x + m - 5 ≥ 0
Tìm điều kiện của m để bất phương trình có nghiệm đúng với ∀x ∈ (0;1).
(2m + 1)x + m - 5 ≥ 0 ⇔ (2m + 1)x ≥ 5 - m (*)
TH1: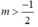 
, bất phương trình (*) trở thành: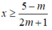 
Tập nghiệm của bất phương trình là:
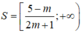
Để bất phương trình đã cho nghiệm đúng với ∀x ∈ (0;1)
thì (0;1)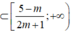 
Hay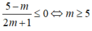 
TH2: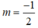 
, bất phương trình (*) trở thành: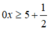 
Bất phương trình vô nghiệm. ⇒ không có m .
TH3: Với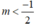 
, bất phương trình (*) trở thành: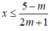 
Tập nghiệm của bất phương trình là:
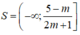
Để bất phương trình đã cho nghiệm đúng với ∀x ∈ (0;1)
thì (0;1)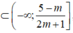 
Hay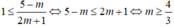 
Kết hợp điều kiện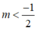 
, ⇒ không có m thỏa mãn.
Vậy với m ≥ 5, bất phương trình đã cho nghiệm đúng với ∀x ∈ (0;1).
Cho bất phương trình m . 3 x + 1 + ( 3 m + 2 ) ( 4 - 7 ) x + ( 4 + 7 ) x > 0
với m là tham số. Tìm tất cả các giá trị của tham số m để bất phương trình đã cho nghiệm đúng với mọi x ∈ ( - ∞ , 0 )
A. m > 2 + 2 3 3
B. m > 2 - 2 3 3
C. m ≥ 2 - 2 3 3
D. m ≥ - 2 - 2 3 3
Cho bất phương trình m . 3 x + 1 + ( 3 m + 2 ) ( 4 - 7 ) x + ( 4 + 7 ) x > 0 với m là tham số. Tìm tất cả các giá trị của tham số m để bất phương trình đã cho có nghiệm đúng với mọi x ∈ - ∞ ; 0
A. m ≥ 2 - 2 3 3
B. m > 2 - 2 3 3
C. m > 2 + 2 3 3
D. m ≥ - 2 - 2 3 3
Đáp án A
Phương pháp: Chia cả 2 vế cho 3x, đặt 
, tìm điều kiện của t.
Đưa về bất phương trình dạng 
Cách giải :
Ta có 
Đặt 
, khi đó phương trình trở thành
Ta có: 
Vậy 
Điều kiện của m để bất phương trình ( 2m+1) x+ m-5 ≥ 0 nghiệm đúng với mọi x thỏa mãn 0< x< 1 :
A. -1/2 < m < 5
B. m = 5
C. m= 5 và m= 1
D. m ≥ 5
Chọn D
Ta có: ( 2m+1) x+ m-5 ≥ 0 tương đương: ( 2m+ 1) x≥ 5- m (*)
+ TH1: Với m> -1/2 , bất phương trình (*) trở thành: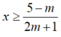 
Tập nghiệm của bất phương trình là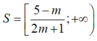 
Để bất phương trình đã cho nghiệm đúng với 0< x< 1 thì 
Hay 
+ TH2: m= -1/ 2, bất phương trình (*) trở thành: 0x ≥ 5+ 1/2
Bất phương trình vô nghiệm. Nên không có m thỏa mãn
+ TH3: Với m< -1/ 2 , bất phương trình (*) trở thành: 
Tập nghiệm của bất phương trình là 
Để bất phương trình đã cho nghiệm đúng với 0< x < 1thì 
Hay 
Kết hợp điều kiện m< -1/ 2 nên không có m thỏa mãn.
Vậy với m ≥ 5, bất phương trình đã cho nghiệm đúng với mọi x: 0< x< 1
Điều kiện của m để bất phương trình (m+ 2) x > 2m2 - 6 (*) nghiệm đúng với mọi x < 1
A. m > -2
B. m = -2
C. m < -2
D. không có m
Chọn D
+ TH1: Với m> - 2 , bất phương trình (*) trở thành: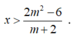 
Tập nghiệm của bất phương trình là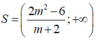 
Để bất phương trình đã cho nghiệm đúng với mọi x < 1thì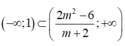 
Suy ra không ra giá trị nào của m thỏa mãn.
+ TH2: m = -2, bất phương trình (*) trở thành: 0x > 2
Bất phương trình vô nghiệm
+ TH3: Với m< - 2 , bất phương trình (*) trở thành: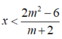 
Tập nghiệm của bất phương trình là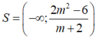 
Để bất phương trình đã cho nghiệm đúng với mọi x< 1thì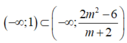 
Hay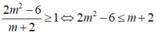 
Kết hợp điều kiện m < -2 không có m
Vậy không có m thỏa mãn.
Tất cả các giá trị của tham số m để bất phương trình (3m+1).12x + (2 - m)6x + 3x < 0 có nghiệm đúng với mọi x > 0 là:
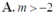
Đáp án B
Đặt t = 2x > 1
PT
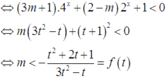
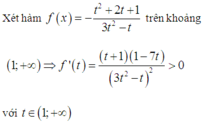
Dựa vào bảng biến thiên, suy ra m < -2
Cho bất phương trình m .3 x + 1 + 3 m + 2 4 − 7 x + 4 + 7 x > 0 , với m là tham số. Tìm tất cả các giá trị của tham số m để bất phương trình đã cho nghiệm đúng với mọi x ∈ − ∞ ; 0 .
A. m > 2 + 2 3 3 .
B. m > 2 − 2 3 3 .
C. m ≥ 2 − 2 3 3 .
D. m ≥ − 2 − 2 3 3 .
Bài 3: Tìm m để bất phương trình: x2 - 2x + 1 - m2 ≤ 0 nghiệm đúng với ∀x ∈ [1; 2]. Bài 4: Tìm m để bất phương trình: (m - 1)x2 + (2 - m)x- 1 > 0 có nghiệm đúng với mọi∀x ∈ (1; 2). Bài 5: Tìm m để bất phương trình: 3(m - 2)x2 + 2(m + 1)x + m - 1 < 0 có nghiệm đúngvới mọi ∀x ∈ (-1; 3). Bài 6: Tìm m để bất phương trình m2 - 2mx + 4 > 0 có nghiệm đúng với mọi ∀x ∈ (-1;0,5)
3:
x^2-2x+1-m^2<=0
=>(x-1)^2-m^2<=0
=>(x-1)^2<=m^2
=>-m<=x-1<=m
=>-m+1<=x<=m+1
mà x thuộc [-1;2]
nên -m+1>=-1 và m+1<=2
=>-m>=-2 và m<=1
=>m<=2 và m<=1
=>m<=1
Tất cả các giá trị của tham số m để bất phương trình 3 m + 1 . 12 x + 2 - m 6 x + 3 x < 0 có nghiệm đúng với mọi x > 0 là:
A. m > -2
B. m < -2
C. m < 1 3
D. - 2 < m < 1 3
Đáp án B
Đặt t = 2 x > 1
PT ⇔ 3 m + 1 . 4 x + 2 - m 2 x + 1 < 0 ⇔ m 3 t 2 - t + t + 1 2 < 0 ⇔ m < - t 2 + 2 t + 1 3 t 2 - t = f ( t )
Xét hàm f ( x ) = - t 2 + 2 t + 1 3 t 2 - t trên khoảng 1 ; + ∞ ⇒ f ' t = t + 1 1 - 7 t 3 t 2 - t 2 > 0 với t ∈ 1 ; + ∞
Dựa vào bảng biến thiên, suy ra m < -2.
