Trên đoạn - 2 π , 5 π 2 , đồ thị hai hàm số y = sin x và y = cos x cắt nhau tại bao nhiêu điểm?
A. 2
B. 4
C. 3
D. 5
Những câu hỏi liên quan
Hàm số y = sinx đồng biến trên đoạn nào dưới đây ?
A . [ π ; 2π ]
B . [-π ; π ]
C . [ 0 ; π ]
D . [ 0 ; \(\dfrac{\pi}{2}\)]
????????????????????
Khi đặt hiệu điện thế không đổi 30 V vào hai đầu đoạn mạch gồm điện trở thuần mắc nối tiếp với cuộn cảm thuần có độ tự cảm 1/4
π
(H) thì dòng điện trong đoạn mạch là dòng điộn một chiều có cường độ 1 A. Nếu đặt vào hai đầu đoạn mạch này điện áp xoay chiều u 150.1/
π
.cos120
π
t(V) thì biểu thức của cường độ dòng điện trong đoạn mạch là :A. i 5
2
cos(120...
Đọc tiếp
Khi đặt hiệu điện thế không đổi 30 V vào hai đầu đoạn mạch gồm điện trở thuần mắc nối tiếp với cuộn cảm thuần có độ tự cảm 1/4 π (H) thì dòng điện trong đoạn mạch là dòng điộn một chiều có cường độ 1 A. Nếu đặt vào hai đầu đoạn mạch này điện áp xoay chiều u = 150.1/ π .cos120 π t(V) thì biểu thức của cường độ dòng điện trong đoạn mạch là :
A. i = 5 2 cos(120 π t + π /4) (A).
B. i = 5 2 cos(120 π t - π /4) (A).
C. i = 5cos(120 π t - π /4) (A).
D. i = 5cos(120 π t + π /4) (A).
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: f(x) = 1/sinx trên đoạn [ π /3; 5 π /6]
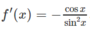
f′(x) < 0 nên và f’(x) > 0 trên ( π /2; 5 π /6] nên hàm số đạt cực tiểu tại x = π /2 và f CT = f( π /2) = 1
Mặt khác, f( π /3) = 2 3 , f(5 π /6) = 2
Vậy min f(x) = 1; max f(x) = 2
Đúng 0
Bình luận (0)
Tìm GTLN, GTNN của hàm số y = sinx + cosx trên đoạn [ π/4 ; π/2 ]
Cho hàm f(x) có đạo hàm trên đoạn
[
0
;
π
]
,
f
(
0
)
π
,
∫
0
π
f
(
x
)
dx
3
π
. Tính
f
(
π
)
Đọc tiếp
Cho hàm f(x) có đạo hàm trên đoạn [ 0 ; π ] , f ( 0 ) = π , ∫ 0 π f ' ( x ) dx = 3 π . Tính f ( π )
Cho hàm f(x) có đạo hàm trên đoạn
[
0
;
π
]
,
f
(
0
)
π
,
∫
0
π
f
(
x
)
dx
3
π
. Tính
f
(
π
)
A.
f
(
π
)
0
B.
f
(...
Đọc tiếp
Cho hàm f(x) có đạo hàm trên đoạn [ 0 ; π ] , f ( 0 ) = π , ∫ 0 π f ' ( x ) dx = 3 π . Tính f ( π )
A. f ( π ) = 0
B. f ( π ) = - π
C. f ( π ) = 4 π
D. f ( π ) = 2 π
Trên đoạn
-
π
;
π
, hàm số
y
sin
x
có mấy điểm cực trị? A. 2 B. 3 C. 4 D. 5
Đọc tiếp
Trên đoạn - π ; π , hàm số y = sin x có mấy điểm cực trị?
A. 2
B. 3
C. 4
D. 5
Trên đoạn - π ; π , hàm số y = sin x có mấy điểm cực trị ?
A. 2
B. 3
C. 4
D. 5
Chọn B.
Phương pháp : Sử dụng đạo hàm và xét dấu đạo hàm để tìm cực trị.
Đúng 0
Bình luận (0)
Trên đoạn [ - π ; π ] phương trình 4sinx-3 = 0 có tất cả bao nhiêu nghiệm?
A. 1
B. 0
C. 2
D. 4
Trên đoạn - π ; π phương trình 4 sin x - 3 = 0 có tất cả bao nhiêu nghiệm?
A. 1
B. 0
C. 2
D. 4
Đáp án C
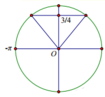
Phương trình đã cho ⇔ sin x = 3 4 ( 1 ) Quan sát đường tròn
lượng giác ta thấy có 2 giá trị của x ∈ - π ; π thỏa mãn phương trình (1).
Đúng 0
Bình luận (0)