Cho tứ diện ABCD, xét điểm M they đổi trên cạnh AB M ≠ A , M ≠ B Gọi (P) là mặt phẳng đi qua M, song song với AC và BD. Thiết diện của tứ diện với mặt phẳng (P) có diện tích lớn nhất thì tỉ số A M A B bằng
A. 1 2
Cho tứ diện ABCD, xét điểm M they đổi trên cạnh AB (M≠A, M≠B). Gọi (P) là mặt phẳng đi qua M, song song với AC và BD. Thiết diện của tứ diện với mặt phẳng (P) có diện tích lớn nhất thì tỉ số AM/AB bằng
A. 1 2
B. 1 3
C. 1 4
D. 3 2
Cho tứ diện ABCD có BCD là tam giác đều cạnh 1, AB = 2. Xét M là điểm thay đổi trên cạnh BC. Mặt phẳng α qua M song song với AB và CD lần lượt cắt các cạnh BD, AD, AC tại N, P, Q. Giá trị nhỏ nhất của biểu thức S = M P 2 + N Q 2 bằng
![]()
![]()
![]()
Cho tứ diện ABCD có BCD là tam giác đều cạnh 1, AB = 2. Xét M là điểm thay đổi trên canh BC. Mặt phẳng (α) qua M song song với AB và CD lần lượt cắt các cạnh BD, AD, AC tại N, P, Q. Giá trị nhỏ nhất của biểu thức S = M P 2 + N Q 2 bằng
A. 8 5
B. 34 9
C. 3 4
D. 8 9
Cho tứ diện đều ABCD có cạnh bằng a,điểm M trên cạnh AB sao cho AM=m(0<m<a). Khi đó diện tích thiết diện của hình tứ diện cắt bởi mp qua M và song song với mp(ACD) là:
A. 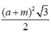
B. ![]()
C. ![]()
D. ![]()
Đáp án B
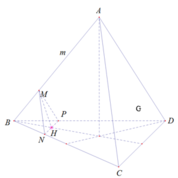
Trong (ABC) kẻ MN // AC ( N ∈ BC)
Trong (ABD) kẻ MP // AD ( P ∈ BD)
⇒ (MNP) là mặt phẳng cần tìm
Xét tam giác MNP có MN = MP =NP (= a - m )
⇒ tam giác MNP đều
Mà NP // CD và BG là trung tuyến tam giác BCD
⇒ BG cắt NP tại H là trung điểm NP
⇒ MH là đường cao tam giác MNP
Ta có: PH = a - m 2 và MP = a – m. Áp dụng định lý pitago, ta có: MH = 3 2 a - m
Và NP = a – m
SMNP = MH . NP 2 = 3 4 a - m 2
Cho tứ diện đều ABCD cạnh a. Các điểm M, N, P, Q thay đổi tương ứng trên cạnh AB. AD, CD, CB. Giá trị nhỏ nhất của tổng MN + NP + PQ + QM là
A. a
B. a 3
C. 2a
D. 3a
Cho tứ diện đều ABCD có độ dài cạnh bằng a, (S) là mặt cầu tiếp xúc với sáu cạnh của tứ diện ABCD, M là điểm thay đổi trên mặt cầu (S). Tính tổng
T = M A 2 + M B 2 + M C 2 + M D 2
A. 3 a 2 8
B. a 2
C. 4 a 2
D. 2 a 2
Cho tứ diện đều ABCD có độ dài cạnh bằng a, (S) là mặt cầu tiếp xúc với sáu cạnh của tứ diện ABCD, M là điểm thay đổi trên mặt cầu (S). Tính tổng T = M A 2 + M B 2 + M C 2 + M D 2 .
A. 3 a 2 8
B. a 2
C. 4 a 2
D. 2 a 2
Đáp án D
Với tứ diện đều ABCD thì mặt cầu (S) là mặt cầu có tâm trùng với tâm của mặt cầu ngoại tiếp tứ diện ABCD và là trọng tâm của tứ diện đều cạnh a, đồng thời có bán kính R = a 2 4
Gọi G là trọng tâm của tứ diện ⇒ G A ¯ + G B ¯ + G C ¯ + G D ¯ = 0 ¯
Ta có:
T = M A 2 + M B 2 + M C 2 + M D 2 = M G ¯ + G A ¯ 2 + M G ¯ + G B ¯ 2 + M G ¯ + G C ¯ 2 + M G ¯ + G D ¯ 2
= 4 M G 2 + 2 M G ¯ G A ¯ + G B ¯ + G C ¯ + G D ¯ ⏟ 0 + G A 2 + G B 2 + G C 2 + G D 2 = 4 M G 2 + 4 G A 2
= 4 a 2 4 2 + 4 a 6 4 2 = 2 a 2 . Vậy T = M A 2 + M B 2 + M C 2 + M D 2 = 2 a 2
Cho hình vuông ABCD có M là 1 điểm thuộc BD. Từ M kẻ ME vuông góc với AB \(\left(E\in AB\right)\)và kẻ MF vuông góc với AD\(\left(F\in AD\right)\). CMR
a) Chu vi của tứ giác AEMF không đổi khi M thay đổi trên cạnh BD
b) EC vuông góc với BF
c) CMR diện tích tứ giác AEMF nhỏ nhất khi M là trung điểm của cạnh BD
Cho hình vuông ABCD. Điểm M thuộc cạnh AB(M khác A và B). Tia CM cắt tia DA tại N. Vẽ Cx vuông góc với CM và cắt tia AB tại E. Gọi H là trung điểm của đoạn NE. Tìm vị trí của điểm M trên cạnh AB để diện tích tứ giác NACE bằng 15/8 diện tích hình vuông ABCD.
Mk chỉ nêu cách làm bạn tự triển khai nha!
CM \(\Delta ADC=\Delta CBE (g.c.g)\) (*)
(\(\angle C_1=\angle C_2\) cùng phụ với \(\angle ACB\))
\(\Rightarrow AC=CE\Rightarrow \Delta ACE \) cân tại C
\(\Rightarrow AB=CE\)
Từ (*) suy ra:
\(S_{ANEC}=S_{ACE}+S_{ANE}=S_{ABCD}+S_{ANE}\)
\(=\dfrac{1}{2}AB^2+\dfrac{1}{2}NA.2AB=\dfrac{1}{2}AB(AB+2NA)\)
Mà \( S_{ANCE}=\dfrac{15}{8} S_{ABCD}\) \(\Rightarrow \dfrac{15}{8}.\dfrac{1}{2} AB^2=\dfrac{1}{2}.AB(2AN+AB)\)
\(\Rightarrow 2AN+AB=\dfrac{15}{8}AB\) \(\Rightarrow \dfrac{NA}{AB}=\dfrac{7}{16}\)
CM \(\Delta NAM \) đồng dạng với \(\Delta CBM\) \((g.g)\)
\(\Rightarrow \dfrac{NA}{AB}=\dfrac{NA}{BC}=\dfrac{AM}{MB}=\dfrac{7}{16}\)
Vậy cần lấy M sao cho \(\dfrac{AM}{MB}=\dfrac{7}{16}\)