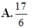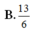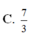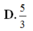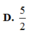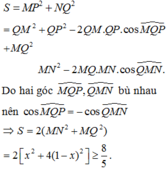Các câu hỏi tương tự
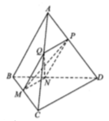
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM x (0 x a) Mặt phẳng (
α
) qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất.
Đọc tiếp
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB = b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM = x (0 < x < a) Mặt phẳng ( α ) qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất.
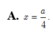
![]()
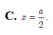
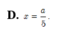
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM x (0 x a). Mặt phẳng (
α
) qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất. A. x
a
4
B. x
a
3
C. x
a
2
D. x ...
Đọc tiếp
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB = b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM = x (0 < x < a). Mặt phẳng ( α ) qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất.
A. x = a 4
B. x = a 3
C. x = a 2
D. x = a 5
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM x (0 x a). Mặt phẳng
(
α
)
qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất.
Đọc tiếp
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB = b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM = x (0 < x< a). Mặt phẳng ( α ) qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất.
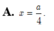
![]()
![]()
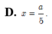
Cho tứ diện SABC có SA vuông góc với mặt phẳng (ABC), SA SB 3 cm, BC 5cm và diện tích tam giác SAC bằng 6
c
m
2
. Một mặt phẳng
α
thay đổi qua trọng tâm G của tứ diện cắt các cạnh AS, AB, AC lần lượt tại M, N, P. Tính giá trị nhỏ nhất
T
m
của biểu thức
T
1...
Đọc tiếp
Cho tứ diện SABC có SA vuông góc với mặt phẳng (ABC), SA= SB= 3 cm, BC =5cm và diện tích tam giác SAC bằng 6 c m 2 . Một mặt phẳng α thay đổi qua trọng tâm G của tứ diện cắt các cạnh AS, AB, AC lần lượt tại M, N, P. Tính giá trị nhỏ nhất T m của biểu thức T = 1 A M 2 + 1 A N 2 + 1 A P 2
A. T m = 8 17
B. T m = 41 144
C. T m = 1 10
D. T m = 1 34
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N là hai điểm thay đổi lần lượt thuộc cạnh BC, BD sao cho mặt phẳng (AMN) luôn vuông góc với mặt phẳng (BCD). Gọi
V
1
;
V
2
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối tứ diện ABMN. Tính
V
1
+
V
2
?
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N là hai điểm thay đổi lần lượt thuộc cạnh BC, BD sao cho mặt phẳng (AMN) luôn vuông góc với mặt phẳng (BCD). Gọi V 1 ; V 2 lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối tứ diện ABMN. Tính V 1 + V 2 ?

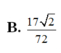
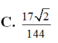
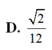
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB 1, AC 2; cạnh bên SA vuông góc với đáy và SA 1. Gọi I là trung điểm của AC. Xét M là điểm thay đổi trên cạnh AB sao cho
A
M
x
(
0
x
1
)
và (P) là mặt phẳng đi qua M, song song với SA và IB. Thiết diện của hình chóp với mặt phẳng (P) có diện tích lớn nhất thì giá trị của x bằng.
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = 1, AC = 2; cạnh bên SA vuông góc với đáy và SA = 1. Gọi I là trung điểm của AC. Xét M là điểm thay đổi trên cạnh AB sao cho A M = x ( 0 < x < 1 ) và (P) là mặt phẳng đi qua M, song song với SA và IB. Thiết diện của hình chóp với mặt phẳng (P) có diện tích lớn nhất thì giá trị của x bằng.
![]()
![]()
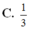
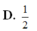
Cho tứ diện ABCD. Gọi I là trung điểm của BC, M là điểm trên cạnh DC. Một mp
α
qua M, song song BC và AI. Gọi P, Q lần lượt là giao điểm của
α
với BD và AD. Xét các mệnh đề sau: (1) MP // BC (2) MQ // AC (3) PQ // AI (4) (MPQ) // (ABC) Số mệnh đề đúng là:
Đọc tiếp
Cho tứ diện ABCD. Gọi I là trung điểm của BC, M là điểm trên cạnh DC. Một mp α qua M, song song BC và AI. Gọi P, Q lần lượt là giao điểm của α với BD và AD. Xét các mệnh đề sau:
(1) MP // BC
(2) MQ // AC
(3) PQ // AI
(4) (MPQ) // (ABC)
Số mệnh đề đúng là:
![]()
![]()
![]()
Cho tứ diện đều S.ABC có cạnh bằng 1. Mặt phẳng (P) đi qua điểm S và trọng tâm G của tam giác ABC cắt các cạnh AB, AC lần lượt tại M, N. Tính thể tích nhỏ nhất Vmin của khối tứ diện SAMN.
Đọc tiếp
Cho tứ diện đều S.ABC có cạnh bằng 1. Mặt phẳng (P) đi qua điểm S và trọng tâm G của tam giác ABC cắt các cạnh AB, AC lần lượt tại M, N. Tính thể tích nhỏ nhất Vmin của khối tứ diện SAMN.
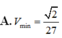
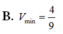
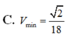
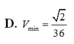
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I là trung điểm cạnh SC. Xét
α
là mặt phẳng thay đổi qua AI và cắt các cạnh SB, SD lần lượt tại M và N. Tổng giá trị nhỏ nhất là lớn nhất của biểu thức
T
S
M
S
B
+
S
N
S
D
bằng
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I là trung điểm cạnh SC. Xét α là mặt phẳng thay đổi qua AI và cắt các cạnh SB, SD lần lượt tại M và N. Tổng giá trị nhỏ nhất là lớn nhất của biểu thức T = S M S B + S N S D bằng