Số nghiệm chung của hai phương trình: 4 cos 2 x - 3 = 0
và 2sinx + 1 = 0 trên khoảng - π 2 ; 3 π 2 bằng:
A. 4
B. 2
C. 3
D. 1
Số nghiệm chung của hai phương trình 4 cos 2 x - 3 = 0 và 2 sin x + 1 = 0 trên khoảng - π 2 ; 3 π 2 bằng:
A. 2
B. 4
C. 3
D. 1
Số nghiệm chung của hai phương trình: 4 cos 2 x - 3 = 0 và 2 sin x + 1 = 0 trên khoảng - π 2 ; 3 π 2 bằng:
![]()
![]()
![]()
![]()
Số nghiệm chung của hai phương trình: 4 cos 2 x − 3 = 0 và 2 sin x + 1 = 0 trên khoảng − π 2 ; 3 π 2 bằng:
A. 4
B. 2
C. 3
D. 1
Đáp án B
Phương pháp:
Sử dụng các công thức giải phương trình lượng giác cơ bản:



Số nghiệm chung của hai phương trình 4 cos 2 x - 3 = 0 và 2 sin x + 1 = 0 trên khoảng ( - π 2 ; 3 π 2 ) bằng
A. 2
B. 4
C. 3
D. 1
Số nghiệm chung của hai phương trình 4 cos 2 x - 3 = 0 và 2 sin x + 1 = 0 trên khoảng - π 2 ; 3 π 2 là
A. 4
B. 1
C. 2
D. 3
Số nghiệm chung của hai phương trình 4 cos 2 x - 3 = 0 và 2sinx + l = 0 trên khoảng (-π/2;3π/2) là?
A. 4.
B. 1.
C. 2.
D. 3.
Sô nghiệm chung của hai phương trình 4 cos 2 x - 3 = 0 và 2sinx+1=0 trên khoảng - π 2 ; 3 π 2 là:
A. 4.
B. 1.
C. 2.
D. 3.
Đáp án C
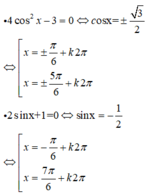
Vậy 2 pt trên có 2 họ nghiệm chung là:
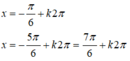
Số nghiệm chung của hai phương trình 4 cos 2 x - 3 = 0 và 2 sin x + 1 = 0 trên khoảng - π 2 ; 3 π 2 là:
A. 4.
B. 1.
C. 2
D. 3.
Đáp án C
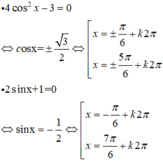
Vậy 2 pt trên có 2 họ nghiệm chung là:
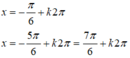
Số nghiệm chung của hai phương trình 4 cos 2 x − 3 = 0 và 2.sin x + 1 = 0 trên khoảng − π 2 ; 3 π 2 là:
A. 4
B. 1
C. 2
D. 3