Hàm số y = 2cosx + x + π 4 sin đạt giá trị lớn nhất là:
A. 5 + 2 2
B. 5
C. 5 - 2 2
D. 5 + 2 2
Tìm giá trị lớn nhất và nhỏ nhất của hàm số : Y= 3/ 2+sin(π/3 +x)
\(sin\left(\dfrac{\pi}{3}+x\right)\in\left[-1;1\right]\)
\(\Rightarrow y=\dfrac{3}{2}+sin\left(\dfrac{\pi}{3}+x\right)\in\left[\dfrac{1}{2};\dfrac{5}{2}\right]\)
\(\Rightarrow\left\{{}\begin{matrix}y_{min}=\dfrac{1}{2}\\y_{max}=\dfrac{5}{2}\end{matrix}\right.\)
Hàm số y = 2 cos x + sin x + π 4 đạt giá trị lớn nhất là
A. 5 + 2 2
B. 5 - 2 2
C. 5 - 2 2
D. 5 + 2 2
Chọn D.
Phương pháp: Biến đổi biểu thức xác định hàm số để đánh giá.
Cách giải: Ta có:
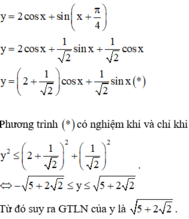
Hàm số y = 2 cos x + sin x + π 4 đạt giá trị lớn nhất là
A. 5 + 2 2
B. 5 - 2 2
C. 5 - 2 2
D. 5 + 2 2
Đáp án D
Ta có: y = 2 cos x + 2 2 sin x + cos x = 2 2 . sin x + 4 + 2 2 . cos x
Áp dụng bất đẳng thức Bunhiacopxki, có
2 2 . sin x + 4 + 2 2 . cos x 2 ≤ 2 2 2 + 4 + 2 2 2 . sin 2 x + cos 2 x = 5 + 2 2
Suy ra y 2 ≤ 5 + 2 2 ⇔ y ≤ 5 + 2 2 . Vậy y m a x = 5 + 2 2 .
Hàm số y = 2 cos x + sin x + π 4 đạt giá trị lớn nhất là
![]()
![]()
![]()
![]()
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 sin x + cos 2x trên đoạn 0 , π . Khi đó 2M + m bằng
A. 4
B. 5/2
C. 7/2
D. 5
Cho hàm số F(x) là một nguyên hàm của hàm số f x = 2 cos x − 1 sin 2 x trên khoảng 0 ; π Biết rằng giá trị lớn nhất của F(x) trên khoảng 0 ; π là 3 . Chọn mệnh đề đúng trong các mệnh đề sau?
A. F π 6 = 3 3 − 4
B. F 2 π 3 = 3 2
C. F π 3 = − 3
D. F 5 π 6 = 3 − 3
Cho hàm số F(x) là một nguyên hàm của hàm số f ( x ) = 2 cos x - 1 sin 2 x trên khoảng 0 ; π . Biết rằng giá trị lớn nhất của F(x) trên khoảng 0 ; π là 3 . Chọn mệnh đề đúng trong các mệnh đề sau?

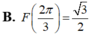
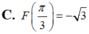
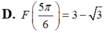
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
a) \(y=f\left(x\right)=\dfrac{4}{\sqrt{5-2\cos^2x\sin^2x}}\)
b)\(y=f\left(x\right)=3\sin^2x+5\cos^2x-4\cos2x-2\)
c)\(y=f\left(x\right)=\sin^6x+\cos^6x+2\forall x\in\left[\dfrac{-\pi}{2};\dfrac{\pi}{2}\right]\)
Cho hàm số y=(3m-4)x\(^2\) với m\(\ne\)\(\dfrac{4}{3}\). Tìm các giá trị của tham số m để hàm số :
a) Đạt giá trị lớn nhất là 0
b) Đạt giá trị nhỏ nhất là 0
a) Để m đạt giá trị lớn nhất là 0 thì \(y=\left(3m-4\right)x^2\le0\) ⇔ \(3m-4\le0\)
⇔ \(m\le\dfrac{4}{3}\) nhưng theo điều kiện
thì m ≠ \(\dfrac{4}{3}\)
➤ Để m đạt giá trị lớn nhất là 0 thì \(m< \dfrac{4}{3}\)
b) Để m đạt giá trị nhỏ nhất là 0 thì \(y=\left(3m-4\right)x^2\ge0\) ⇔ \(3m-4\ge0\)
⇔ \(m\ge\dfrac{4}{3}\) nhưng theo điều kiện
thì m ≠ \(\dfrac{4}{3}\)
➤ Để m đạt giá trị nhỏ nhất là 0 thì \(m>\dfrac{4}{3}\)