Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng?
A. 2
B. 6
C. 8
D. 4
Những câu hỏi liên quan
cho hình chóp tứ giác đều biết cạch đáy bằng 30 cm trung đoạn bằng 10 cm tính diện tích toàn phần của hình chóp tứ giác đều
các bạn giúp mình nha !!
cho tứ giác đều s.abcd với các kích thước sh là chiều cao , sc = 5cm , si là trung điểm của tam giác cân bên sbc , ab= 6cm
a , tính trung đoạn của hình chóp ( si)
b tính chu vi đáy hình chóp
c , tính diện tích xung quanh hình chóp
d, thể tích hình chóp
Một hình chóp tứ giác đều có độ dài cạnh bên bằng 25cm, đáy là hình vuông ABCD cạnh 30cm.
Tính diện tích toàn phần của hình chóp.
Các câu sau đúng hay sai?Vì sao?
A)tứ giác có 4 góc đều nhọn
B)tứ giác có 4 góc đều vuông
C)tứ giác có 4 góc đều từ
Đ)tứ giác có nhiều nhất 3 góc nhọn
Giúp mk nha.Cảm ơn trước
a,b,c sai còn d đúng
Giải thích vẽ hình ra sẽ thấy
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD, đấy là hình vuông cạnh bằng 10cm, biết SA=13cm. Tính diện tích xung quanh và diện tích toàn phần và thể tích của hình chóp trên.
Ta có:
AI=\(\dfrac{AB}{2}=5cm\)
Áp dụng định lý Pitago vào △SIA
⇒ SI2+AI2=SA2 ⇒ SI=√(SA2-AI2)=12 cm
nên Sxq ABCD=p.d=\(\dfrac{1}{2}\).10.4.12=240 cm2
Áp dụng định lý Pitago vào △ABC
⇒ AC2=AB2+BC2 ⇒ AC=√(102+102)=10√2 cm
Ta có: OA=\(\dfrac{AC}{2}\)=5√2 cm
Áp dụng định lý Pitago vào △SOA
⇒ SA2=SO2+SA2 ⇒ SO=√[132-(5√2)2]=√119 cm
nên VABCD=\(\dfrac{1}{3}\).10.4.√119≈145,45 cm3
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy và SA a. Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC. A.
3
πa
2
7
B.
7
πa
2
12
C.
7...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy và SA = a. Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC.
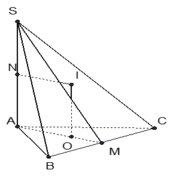
A. 3 πa 2 7
B. 7 πa 2 12
C. 7 πa 2 3
D. πa 2 7
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy và SA = a. Tính thể tích V của mặt cầu ngoại tiếp hình chóp S.ABC.
Gọi M là trung điểm SA và O là tâm đáy \(\Rightarrow AO=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\) ; \(AM=\dfrac{a}{2}\)
Qua O kẻ đường thẳng d song song SA, trong mặt phẳng (SAO) qua M kẻ đường thẳng song song AO cắt d tại I
\(\Rightarrow I\) là tâm mặt cầu ngoại tiếp chóp
\(R=IA=\sqrt{IM^2+AM^2}=\sqrt{AO^2+AM^2}=\dfrac{a\sqrt{21}}{6}\)
Đúng 1
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy, cho elíp :
E
:
x
2
4
+
y
2
1
và điểm C( 2;0) .Tìm tọa độ các điểm A; B trên (E), biết rằng hai điểm đối xứng nhau qua trục hoành và tam giác ABC là tam giác đều và điểm A có tung độ dương .
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy, cho elíp : E : x 2 4 + y 2 = 1 và điểm C( 2;0) .Tìm tọa độ các điểm A; B trên (E), biết rằng hai điểm đối xứng nhau qua trục hoành và tam giác ABC là tam giác đều và điểm A có tung độ dương .
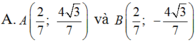
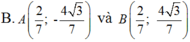
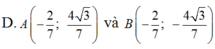
Đáp án A
Giả sử A( x0 ; y0) , Do A ; B đối xứng nhau qua Ox nên B( x0 ; -y0).
Ta có:
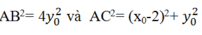
Vì A thuộc (E) nên:
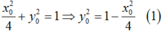
Vì AB = AC nên:
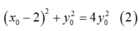
Thay (1) vào (2) ta được:
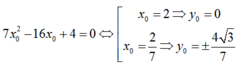
Vì điểm A khác C và Acó tung độ dương nên:
Đúng 0
Bình luận (0)
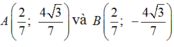
Cho hình chóp tứ giác đều SABCD có đáy ABCD là hình vuông cạnh bằng a, mặt bên hợp với mặt đáy góc 60 độ. Gọi M,N là trung điểm các cạnh AB và SD. Tính theo a thể tích của khối chóp SABCD và khoảng cách giữa MN,CD.