Cho hình lăng trụ tam giác đều ABC.A’B’C’có cạnh đáy bằng 2a, khoảng cách từ A đến mặt phẳng (A’BC) bằng a 6 2 . Thể tích của khối lăng trụ đã cho bằng
Đáp án A.
Gọi M là trung điểm của BC. Trong mặt phẳng (AA’M), kẻ AH ⊥ A'M.
ΔA’BC cân tại A
ΔAA’M vuông tại A
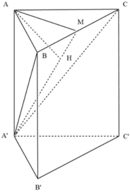
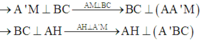
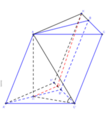
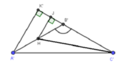
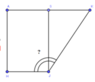
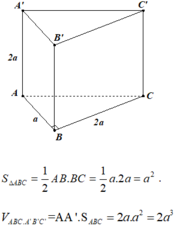
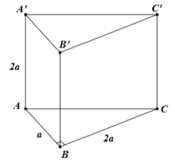
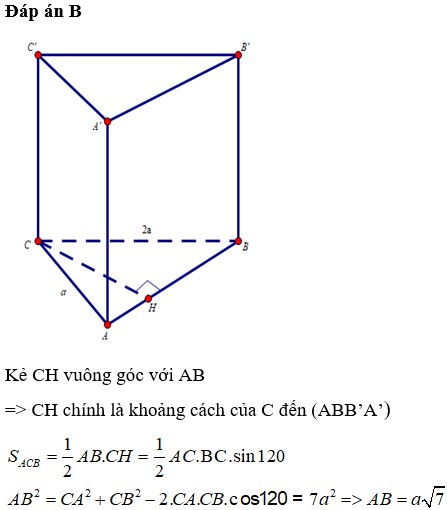
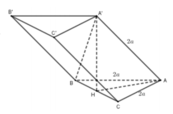
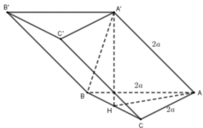
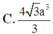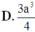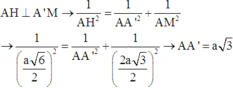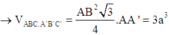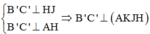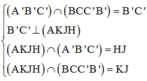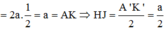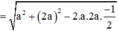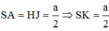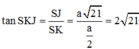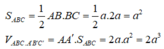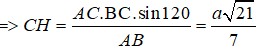Cho lăng trụ ABC.A’B’C’có AB = 2a, BC = 2a, góc A’B’C’ = 120 0 . Hình chiếu vuông góc của A trên mặt phẳng (A’B’C’) trung với điểm của A’B’. Góc giữa đường thẳng AC’ và mặt phẳng (A’B’C’) bằng 60 0 . Gọi α là góc giữa hai mặt phẳng (BCC’B’) và (ABC). Khi đó, tan α có giá trị là:
A. 21
B. 2 2
C. 21 2
D. 2 21
Đáp án D
Phương pháp: Cho hai mặt phẳng (α) và (β) cắt nhau, ta xác định góc giữa (α) và (β) như sau:
- Tìm giao tuyến ∆ của hai mặt phẳng (α) và (β).
- Tìm trong mỗi mặt phẳng (α), (β) một đường thẳng 𝑎, cùng cùng vuông góc với ∆ và cùng cắt ∆ tại điểm .
- Xác định góc giữa 𝑎 và 𝑏.
Cách giải: Gọi H là trung điểm của A’B’ => AH ⊥ (A’B’C’)
Kẻ HJ, A'K' ⊥ B'C', (J, K' ∈ B'C'), AK ⊥ BC, (K ∈ BC)
HJ//A'K', A'K'//AK => HJ//AK => H,J,A,K đồng phẳng
Vì 
Ta có: 
=> ((BCC'B');(A'B'C')) = (KJ;HJ)
A ' B ' K ' ^ = 180 0 - 120 0 = 60 0
=> A'K' = A'B' . sin 60 0
Xét ∆B’HC’ : H'C = 
∆AHC’ vuông tại H => AH = HC.tanC’ = HC.tan(AC’;(A’B’C’)) (vì AH ⊥ (A’B’C’))
Xét hình thang vuông AKJH:
Kẻ 
Vì AK//HJ
Cho hình lăng trụ đứng ABC.A'B'C' có AA'=2a, tam giác ABC vuông tại B có AB=a; BC=2a. Thể tích khối lăng trụ ABC.A'B'C' là
A. 2 a 3
B. 2 a 3 3
C. 4 a 3 3
D. 4 a 3
Cho hình lăng trụ đứng ABC.A'B'C' có AA' = 2a, tam giác ABC vuông tại B, có AB = a, BC = 2a. Thể tích khối lăng trụ là ABC.A'B'C'
A. 2 a 3
B. 2 a 3 3
C. 4 a 3 3
D. 4 a 3
Cho hình lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(B\), \(AA' = 2a,AD = 2a,AB = BC = a\).
a) Tính độ dài đoạn thẳng \(AC'\).
b) Tính tổng diện tích các mặt của hình lăng trụ.
a) \(\Delta ABC\) vuông cân tại \(B \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)
\(CC' = AA' = 2a\)
\(CC' \bot \left( {ABCD} \right) \Rightarrow CC' \bot AC\)
\( \Rightarrow \Delta ACC'\) vuông tại \(C \Rightarrow AC' = \sqrt {A{C^2} + CC{'^2}} = a\sqrt 6 \)
b) \({S_{ABC{\rm{D}}}} = {S_{A'B'C'C'}} = \frac{1}{2}\left( {A{\rm{D}} + BC} \right).AB = \frac{{3{a^2}}}{2}\)
Gọi \(M\) là trung điểm của \(AD\)
\( \Rightarrow ABCM\) là hình vuông\( \Rightarrow MC = M{\rm{D}} = MA = \frac{1}{2}A{\rm{D}} = a\)
\(\Delta MC{\rm{D}}\) vuông cân tại \(M \Rightarrow C{\rm{D}} = \sqrt {C{M^2} + D{M^2}} = a\sqrt 2 \)
\(\begin{array}{l}{S_{ABB'A'}} = AB.AA' = 2{a^2}\\{S_{ADD'A'}} = AD.AA' = 4{a^2}\\{S_{BCC'B'}} = BC.CC' = 2{a^2}\\{S_{C{\rm{DD}}'{\rm{C}}'}} = C{\rm{D}}.CC' = 2{a^2}\sqrt 2 \end{array}\)
Tổng diện tích các mặt của hình lăng trụ là:
\(\begin{array}{l}S = {S_{ABC{\rm{D}}}} + {S_{A'B'C'C'}} + {S_{ABB'A'}} + {S_{ADD'A'}} + {S_{BCC'B'}} + {S_{C{\rm{DD}}'{\rm{C}}'}}\\ & = \frac{{3{a^2}}}{2} + \frac{{3{a^2}}}{2} + 2{a^2} + 4{a^2} + 2{a^2} + 2{a^2}\sqrt 2 = \left( {11 + 2\sqrt 2 } \right){a^2}\end{array}\)
Cho hình lăng trụ đứng ABC. A'B'C' có AC=a, BC=2a, A C B ^ = 120 ° . Tính khoảng cách từ điểm C tới mặt phẳng (ABB'A')
A. a 12 7
B. a 21 7
C. a 7 21
D. a 7 12
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, AB=2a, BC=a. Biết thể tích khối lăng trụ ABC.A’B’C’ bằng a 3 , chiều cao của hình lăng trụ đã cho bằng
A. a/2.
B. a.
C. 3a.
D. 3a/2.
Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác vuông cân đỉnh A , AB = 2a, AA' = 2a, hình chiếu vuông góc của A' lên mặt phẳng (ABC) là trung điểm H của cạnh BC . Thể tích của khối lăng trụ ABC.A'B'C' bằng
A. 4 a 3 2
B. 2 a 3 2
C. a 3 14 4
D. 2 a 3 2 3
Phương pháp
- Tính chiều cao A 'H .
- Tính thể tích khối lăng trụ V = S A B C . A ' H
Cách giải:
Tam giác ABC vuông cân đỉnh A cạnh AB = AC = 2a nên BC 
Tam giác AHA' vuông tại H nên
Vậy thể tích khối lăng trụ
Chọn B.
Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác vuông cân đỉnh A , AB = 2a, AA' = 2a, hình chiếu vuông góc của A' lên mặt phẳng (ABC) là trung điểm H của cạnh BC . Thể tích của khối lăng trụ ABC.A'B'C' bằng
A. 4 a 3 2
B. 2 a 3 2
C. a 3 14 4
D. 2 a 3 2 3
