Gọi F(x) là một nguyên hàm của hàm số y = ln x x .
Nếu F e 2 = 4 t h ì ∫ ln x x d x b ằ n g
A. F x = ln 2 x 2 + C
B. F x = ln 2 x 2 + 2
C. F x = ln 2 x 2 - 2
D. F x = ln 2 x 2 + x + C
Gọi F(x) là một nguyên hàm của hàm số y = ln x x .
Nếu F e 2 = 4 t h ì ∫ ln x x d x b ằ n g
A. F x = ln 2 x 2 + C
B. F x = ln 2 x 2 + 2
C. F x = ln 2 x 2 - 2
D. F x = ln 2 x 2 + x + C
Biết F ( x ) là một nguyên hàm của hàm số f ( x ) = ln 2 x + 1 . ln x x thoả mãn F ( 1 ) = 1 3 . Giá trị của F 2 ( e ) là
A. 8 9
B. 1 9
C. 8 3
D. 1 3
Chọn A
Đặt t = ln 2 x + 1 ⇒ t 2 = ln 2 x + 1 ⇒ t d t = ln x x d x
∫ ln 2 x + 1 . ln x x d x = ∫ t 2 d t = t 3 3 + C = ln 2 x + 1 3 3 + C
Vì F ( 1 ) = 1 3 nên C = 0
Vậy F 2 ( e ) = 8 9
Cho F(x) là một nguyên hàm của hàm số f(x)=x ln x Tính F ' ' x
A. F ' ' x = 1 − ln x
B. F ' ' x = 1 x
C. F ' ' x = 1 + ln x
D. F ' ' x = x + ln x
Đáp án C
Ta có F ' ' x = f ' x = 1 + ln x
Hàm số F(x) = ln|sin x – cos x| là một nguyên hàm của hàm số
A. f ( x ) = sin x + cos x sin x - cos x
B. f ( x ) = sin x - cos x sin x + cos x
C. f ( x ) = 1 sin x + cos x
D. f ( x ) = 1 sin x - cos x
Chọn A.
F ' ( x ) = sin x - cos x ' sin x - cos x = cos x + sin x sin x - cos x
Cho hàm số f(x)=1/x. Nếu F(x) là một nguyên hàm của hàm số f(x) và đồ thị hàm số y=F(x) đi qua M(-1;0) thì F(x) là
![]()
![]()
![]()
![]()
Tính đạo hàm cấp hai của mỗi hàm số sau:
a) \(y = 2{x^4} - 3{x^3} + 5{x^2}\)
b) \(y = \frac{2}{{3 - x}}\)
c) \(y = \sin 2x\cos x\)
d) \(y = {e^{ - 2x + 3}}\)
e) \(y = \ln (x + 1)\)
f) \(y = \ln ({e^x} + 1)\)
\(a,y'=8x^3-9x^2+10x\\ \Rightarrow y''=24x^2-18x+10\\ b,y'=\dfrac{2}{\left(3-x\right)^2}\\ \Rightarrow y''=\dfrac{4}{\left(3-x\right)^3}\)
\(c,y'=2cos2xcosx-sin2xsinx\\ \Rightarrow y''=-5sin\left(2x\right)cos\left(x\right)-4cos\left(2x\right)sin\left(x\right)\\ d,y'=-2e^{-2x+3}\\ \Rightarrow y''=4e^{-2x+3}\)
e,
\(y = \ln (x + 1) \Rightarrow y' = \frac{1}{{x + 1}} \Rightarrow y'' = - \frac{1}{{{{\left( {x + 1} \right)}^2}}}\)
f,
\(y = \ln ({e^x} + 1) \Rightarrow y' = \frac{{{e^x}}}{{{e^x} + 1}} \Rightarrow y'' = - \frac{{{e^x}.{e^x}}}{{{{\left( {{e^x} + 1} \right)}^2}}} = - \frac{{{e^{2x}}}}{{{{\left( {{e^x} + 1} \right)}^2}}}\)
Họ nguyên hàm của hàm số f(x) = 2x ( 2 + ln x) là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Kí hiệu F (x) là một nguyên hàm của hàm số f ( x ) = 1 e x + 1 , biết F 0 = - ln 2 . Tìm tập nghiệm S của phương trình F ( x ) + ln ( e x + 1 ) = 3 .
A. S = - 3 ; 3
B. S = 3
C. S = ∅
D. S = - 3
Đáp án B
∫ 1 e x + 1 d x = ∫ d x - ∫ e x e x + 1 d x = x - ln ( e x + 1 ) + C
Vì F ( 0 ) = = - ln 2 ⇔ C = 0 ⇒ F ( x ) = x - ln e x + 1
Xét phương trình F ( x ) + ln ( e x + 1 ) = 3 ⇔ x = 3
Cho hàm số f(x) liên tục trên khoảng (-2; 3). Gọi F(x) là một nguyên hàm của f(x) trên khoảng (-2; 3). Tính 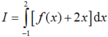 , biết F(-1) = 1, F(2) = 4.
, biết F(-1) = 1, F(2) = 4.
A. I = 6.
B. I = 10.
C. I = 3.
D. I = 9.