Cho hàm số y = x 3 - 3 x 2 + 1 . Tích của giá trị cực đại và cực tiểu của hàm số bằng bao nhiêu?
A. -6
B. -3
C. 3
D. 4
Cho hàm số y = - x 3 + 3 x 2 + 3 ( m 2 - 1 ) x - 3 m 2 - 1 . Có bao nhiêu giá trị nguyên của m để đồ thị hàm số có điểm cực đại và điểm cực tiểu nằm bên trái đường thẳng x=2
A. 3
B. 1
C. 2
D. 0
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = - x 3 + 3 x 2 + 3 ( m 2 - 1 ) x - 3 m 2 - 1 có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số cách đều gốc tọa độ O.
A. 0
B. 1
C. 2
D. 3
+ Đạo hàm y’ = -3x2+ 6x+ 3( m2-1) = -3( x2- 2x-m2+1).
Đặt g( x) = x2- 2x-m2+1 là tam thức bậc hai có ∆ ' = m 2 .
+ Do đó hàm số đã cho có cực đại cực tiểu khi và chỉ khi y’ =0 có hai nghiệm phân biệt hay g(x) =0 có hai nghiệm phân biệt
⇔ ∆ ' > 0 ⇔ m ≠ 0 . (1)
+ Khi đó y’ có các nghiệm là: 1±m .
Tọa độ các điểm cực trị của đồ thị hàm số là A( 1-m ; -2-2m3) và B( 1+m ; -2+ 2m3).
Ta có:
O A → ( 1 - m ; - 2 - 2 m 3 ) ⇒ O A 2 = ( 1 - m ) 2 + 4 ( 1 + m 3 ) 2 . O B → ( 1 + m ; - 2 + 2 m 3 ) ⇒ O B 2 = ( 1 + m ) 2 + 4 ( 1 - m 3 ) 2 .
Để A và B cách đều gốc tọa độ khi và chỉ khi OA= O B hay OA2= OB2
( 1 - m ) 2 + 4 ( 1 + m 3 ) 2 = ( 1 + m ) 2 + 4 ( 1 - m 3 ) 2 ⇔ - 4 m + 16 m 3 = 0
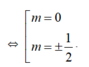
Đối chiếu với điều kiện (1), ta thấy chỉ m = ± 1 2 thỏa mãn yêu cầu bài toán.
Vậy không có giá trị nguyên nào của m thỏa mãn yêu cầu bài toán.
Chọn A.
Cho hàm số y = x 3 - 3 x 2 + 1 . Tích các giá trị cực đại và giá trị cực tiểu của hàm số bằng
A. -6
B. -3
C. 0
D. 3
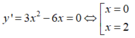
Ta có: y(0) = 1; y(2) = -3
Lập bảng biến thiên suy ra,Hàm số có giá trị cực đại bằng 1 và giá trị cực tiểu bằng -3. Tích của giá trị cực đại và giá trị cực tiểu bằng -3.
Chọn B
Cho hàm số y = a x 3 + b x 2 + c x + d đạt cực đại tại x = -2 với giá trị cực đại là 64; đạt cực tiểu tại x = 3 với giá trị cực tiểu là -61. Khi đó giá trị của a + b + c + d bằng
A. 1
B. 7
C. -17
D. 5
Ta có 64 = -8a + 4b - 2c + d; -61 = 27a + 9b + 3c +d
Từ y ' = 3 a x 2 + 2 b x + c ta thu được hai phương trình 0 = 12a - 4b + c; 0 = 27a + 6b + c
Giải hệ gồm 4 phương trình trên ta thu được a = 2; b = -3; c = -36; d = 20 hay a + b + c + d = -17
Đáp án C
Cho hàm số \(y=x^3-3x^2+m^2x+m\). Tìm tất cả các giá trị của tham số m để hàm số có cực đại, cực tiểu và các điểm cực đại, cực tiểu của đồ thị hàm số đối xứng nhau qua đường thẳng d:\(y=\frac{1}{2}x-\frac{5}{2}\)
Ta có : \(y'=3x^2-6x+m^2\Rightarrow y'=0\Leftrightarrow3x^2-6x+m^2=0\left(1\right)\)
Hàm số có cực trị \(\Leftrightarrow\left(1\right)\) có 2 nghiệm phân biệt \(x_1;x_2\)
\(\Leftrightarrow\Delta'=3\left(3-m^2\right)>0\Leftrightarrow-\sqrt{3}< m< \sqrt{3}\)
Phương trình đường thẳng d' đi qua các điểm cực trị là : \(y=\left(\frac{2}{3}m^2-2\right)x+\frac{1}{3}m^2\)
=> Các điểm cực trị là :
\(A\left(x_1;\left(\frac{2}{3}m^2-2\right)x_1+\frac{1}{3}m^2+3m\right);B\left(x_2;\left(\frac{2}{3}m^2-2\right)x_2+\frac{1}{3}m^2+3m\right);\)
Gọi I là giao điểm của hai đường thẳng d và d' :
\(\Rightarrow I\left(\frac{2m^2+6m+15}{15-4m^2};\frac{11m^2+3m-30}{15-4m^2}\right)\)
A và B đối xứng đi qua d thì trước hết \(d\perp d'\Leftrightarrow\frac{2}{3}m^2-2=-2\Leftrightarrow m=0\)
Khi đó \(I\left(1;-2\right);A\left(x_1;-2x_1\right);B\left(x_2;-2x_2\right)\Rightarrow I\) là trung điểm của AB=> A và B đối xứng nhau qua d
Vậy m = 0 là giá trị cần tìm
Cho hàm số ![]() . Tích các giá trị cực đại và cực tiểu của hàm số bằng:
. Tích các giá trị cực đại và cực tiểu của hàm số bằng:
A. 0
B. -12
C. 20
D. 12
Tìm số mệnh đề sai trong những mệnh đề sau
(1). Nếu hàm số f x đạt cực đại tại x0 thì x0 được gọi là điểm cực đại của hàm số.
(2). Giá trị cực đại (giá trị cực tiểu) của hàm số còn được gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.
(3). Cho hàm số f x là hàm số bậc 3, nếu hàm số có cực trị thì đồ thị hàm số cắt trục Ox tại 3 điểm phân biệt.
(4). Cho hàm số f x là hàm số bậc 3, nếu hàm số cắt trục Ox tại duy nhất một điểm thì hàm số không có cực trị.
A. 2
B. 3
C. 1
D. 4
Đáp án A
Có 2 mệnh đề sai là mệnh đề (3) và mệnh đề (4).
Mệnh đề (3) sai vì nếu hai cực trị của hàm số cùng dấu thì đồ thị hàm số chỉ cắt trục Ox tại một điểm.
Mệnh đề (4) sai lý do tương tự mệnh đề (3).
Cho hàm số y= mx^2 +2(m^2-5)x^4 +4 . Có bao nhiêu số nguyên m để hàm số có 3 điểm cực trị trong đó có đúng 2 điểm cực đại và 1 điểm cực tiểu.
Đề đúng là \(y=mx^2+2\left(m^2-5\right)x^4+4\) chứ bạn (nghĩa là ko bị nhầm lẫn vị trí \(x^2\) và \(x^4\))
Hàm có đúng 2 điểm cực đại và 1 điểm cực tiểu khi:
\(\left\{{}\begin{matrix}2\left(m^2-5\right)< 0\\2\left(m^2-5\right).m< 0\end{matrix}\right.\)
\(\Leftrightarrow0< m< \sqrt{5}\)
\(\Rightarrow\) có 2 giá trị nguyên của m thỏa mãn
Cho hàm số f(x) xác định trên D = [ 0 ; 10 ) \ { 1 } có bảng biến thiên như hình vẽ, trong các mệnh đề sau có bao nhiêu mệnh đề đúng.
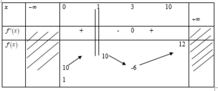
i. Hàm số có cực tiểu là 3.
ii. Hàm số đạt cực đại tại x=1 .
iii. Hàm số có giá trị cực đại là 12.
iv. Hàm số có cực tiểu là -6 .
A. 0
B. 1
C. 2
D. 3