I.

1. Yes, he does.

2. They lie on the grass, looking at the sky and daring each other to find the Milky Way.

3. I like to live in the countryside because it is peaceful and tranquil. (bạn có thể tự đưa suy nghĩ của bản thân vào nha).

II.

1 from

2 is

3 teaching

4 in

5 practise

6 test

7 class

8 at

9 other

10 little

D.

I. 

1. In the 1970s, skateboarding suddenly became very popular.

2. At first, skateboarders moved slowly on flat, smooth areas.

3. Then they began to ride quickly. This is called "freestyle" skateboarding.

4. Soon they were skateboarding skillfully up ramps and doing tricks in the air.

II.

1. Your house is not as small as my house.

2. I like listening to music.

3. The white dress is not as expensive as the black one.

4. Mary is the most intelligent in my group.

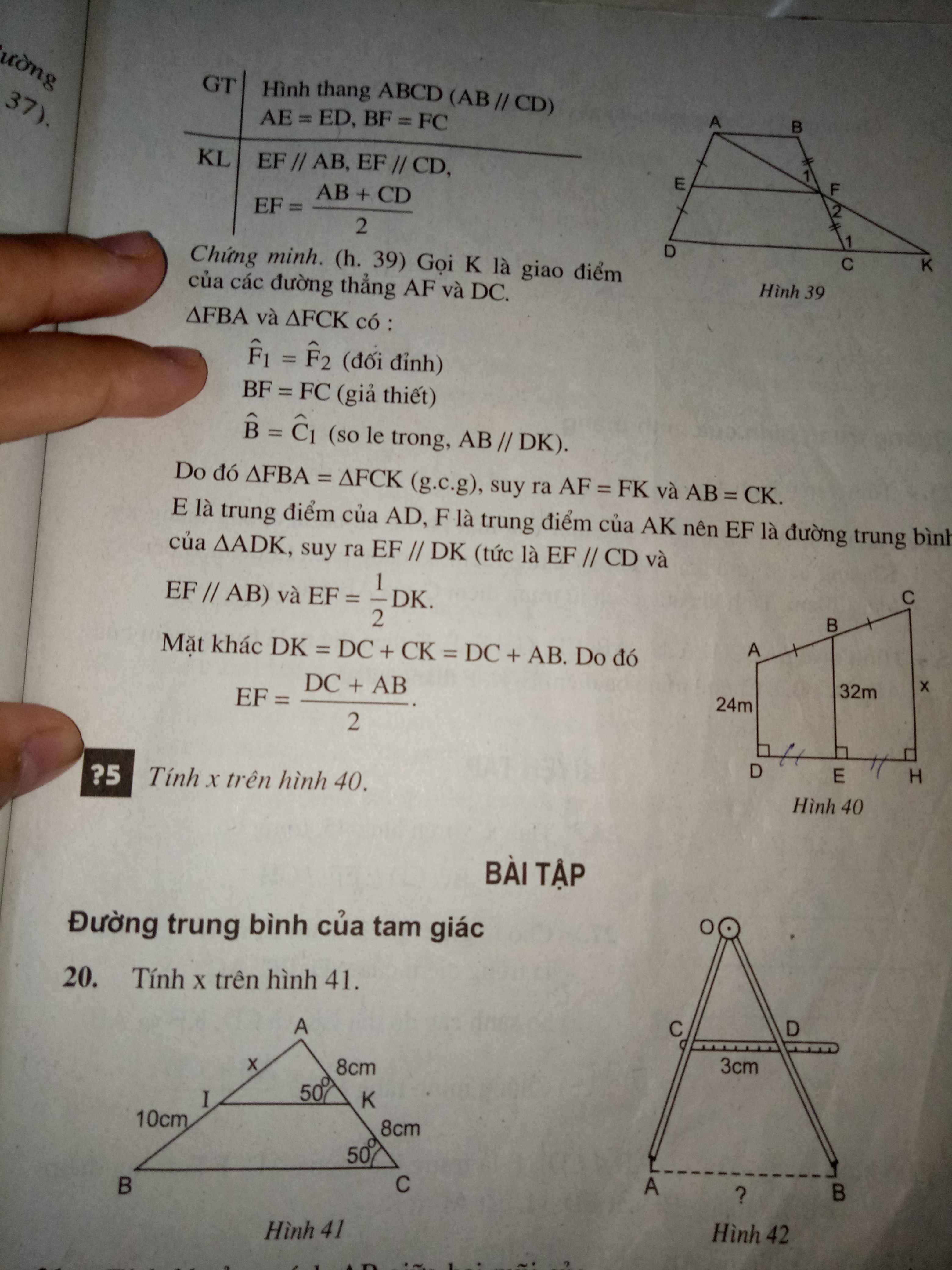
Bài 20

Ta có: \(\widehat{AKI}=\widehat{ACB}=50^0\)(giả thiết) mà hai góc này ở vị trí đồng vị nên IK//BC (dấu hiệu nhận biết hai đường thẳng song song)

Mà KA=KC=8cm suy ra KK là trung điểm của AC.

Từ đó áp dụng định lí: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba.

Ta suy ra được II là trung điểm của AB.

⇒IA=IB=10cm⇒x=10cm

Bài 23

Ta có:  (giả thiết), IK//MP//NQ (vì cùng vuông góc với )

Do đó  là hình thang có hai đáy là và . 

Ta thấy đường thẳng  đi qua trung điểm  của cạnh bên  và song song với hai đáy 

 là trung điểm của  ( Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai).

 (tính chất trung điểm)

Vậy 

bài 24

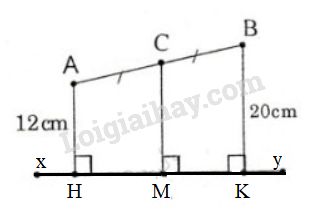
Kẻ  vuông góc với  ( là chân đường vuông góc). 

⇒AH//CM//BK(cùng vuông góc với đường thẳng )

 Tứ giác là hình thang (dấu hiệu nhận biết hình thang)

Xét hình thang có:  (giả thiết)

CM//AH//BK (chứng minh trên)

Suy ra  (Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai)

 là đường trung bình của hình thang  (dấu hiệu nhận biết đường trung bình của hình thang)

BẠN ƠI BẠN CHO MÌNH LÀM QUEN VỚIIIIIIIIIIII

Trước nekkkkkkkkkkkkkkkk!!!!!!!!!!!!!!!!!!!!!!!

(\(x\) + 2).(\(x\) - 4) = 0

\(\left[{}\begin{matrix}x+2=0\\x-4=0\end{matrix}\right.\)

\(\left[{}\begin{matrix}x=-2\\x=4\end{matrix}\right.\)

Vậy \(x\) \(\in\) {-2; 4}

TH1: x + 2 = 0
         x       = 0 - 2

         x       = -2

TH2: x - 4 = 0

         x      = 0 - 4

         x      = -4

Vậy ...

Chúc bạn học tốt nhé

x=-2;4

Ờ thì giúp tội tui ko tên thắng :))

Ta có: \(a+b+c=\sqrt{\left(a+b+c\right)^2}\)

\(=\sqrt{a^2+b^2+c^2+2ab+2bc+2ca}\ge\sqrt{3\left(ab+bc+ca\right)}=3\)

Sau đó áp dụng BĐT AM-GM và Holder ta có:

\(Σ\dfrac{a^2}{\sqrt{3b^2+bc}}=Σ\dfrac{4a^2}{2\sqrt{4b\left(3b+c\right)}}\geΣ\dfrac{4a^2}{7b+c}\)

\(=Σ\dfrac{4a^3}{7ab+ac}\ge\dfrac{4\left(a+b+c\right)^3}{3Σ\left(7ab+ac\right)}=\dfrac{\left(a+b+c\right)^3}{18}\ge\dfrac{3}{2}\)

Xảy ra khi \(a=b=c=1\)

Never nerf :|, cũng xài Holder nhưng theo hướng khác :v

Áp dụng BĐT Holder ta có:

Đặt \(P=\dfrac{a^2}{\sqrt{3b^2+bc}}+\dfrac{b^2}{\sqrt{3c^2+ca}}+\dfrac{c^2}{\sqrt{3a^2+ab}}\)

\(P^2\left[a^2\left(3b^2+bc\right)+b^2\left(3c^2+ca\right)+c^2\left(3a^2+ab\right)\right]\ge\left(a^2+b^2+c^2\right)^3\)

Giờ chứng minh \(\left(a^2+b^2+c^2\right)^3\ge\dfrac{9}{4}\left[a^2\left(3b^2+bc\right)+b^2\left(3c^2+ca\right)+c^2\left(3a^2+ab\right)\right]\)

\(\Leftrightarrow4\left(a^2+b^2+c^2\right)^3\ge9\left[a^2\left(3b^2+bc\right)+b^2\left(3c^2+ca\right)+c^2\left(3a^2+ab\right)\right]\)

\(\Leftrightarrow4\left(a^2+b^2+c^2\right)^3\ge3\left(ab+bc+ca\right)\left[a^2\left(3b^2+bc\right)+b^2\left(3c^2+ca\right)+c^2\left(3a^2+ab\right)\right]\)

Lại có BĐT quen thuộc \(a^2+b^2+c^2\ge ab+bc+ca\)

Nên chỉ ra \(4\left(a^2+b^2+c^2\right)^2\ge3\left[a^2\left(3b^2+bc\right)+b^2\left(3c^2+ca\right)+c^2\left(3a^2+ab\right)\right]\)

Điều này đúng vì

\(4\left(a^2+b^2+c^2\right)^2\ge12\left(a^2b^2+b^2c^2+c^2a^2\right)=3\left(4a^2b^2+4b^2c^2+4c^2a^2\right)\)

\(\ge3\left(3a^2b^2+a^2bc+3b^2c^2+ab^2c+3c^2a^2+abc^2\right)\)

\(=3\left[a^2\left(3b^2+bc\right)+b^2\left(3c^2+ca\right)+c^2\left(3a^2+ab\right)\right]\)

dài thế...

Dài quá!^^

lm từg cái thôi nhé

lam tung phan 1 nhe mai minh hoc roi