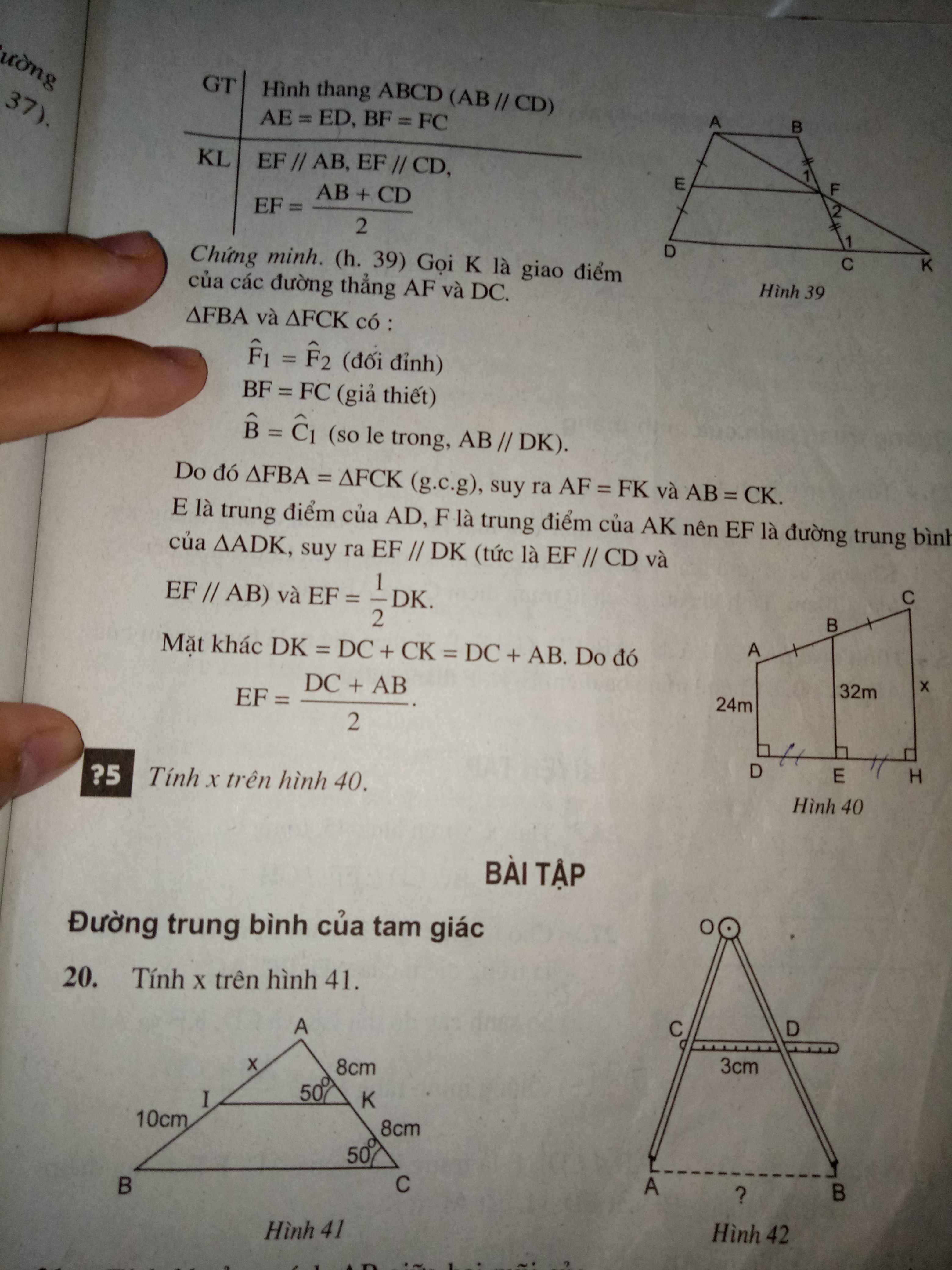
Bài 20
Ta có: \(\widehat{AKI}=\widehat{ACB}=50^0\)(giả thiết) mà hai góc này ở vị trí đồng vị nên IK//BC (dấu hiệu nhận biết hai đường thẳng song song)
Mà KA=KC=8cm suy ra KK là trung điểm của AC.
Từ đó áp dụng định lí: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba.
Ta suy ra được II là trung điểm của AB.
⇒IA=IB=10cm⇒x=10cm
Bài 23
Ta có: IM=IN (giả thiết), IK//MP//NQ (vì cùng vuông góc với PQ)
Do đó MNQP là hình thang có hai đáy là NQvà MP.
Ta thấy đường thẳng IK đi qua trung điểm II của cạnh bên MN và song song với hai đáy NQ,MP
⇒K là trung điểm của PQ ( Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai).
⇒PK=KQ=5dm (tính chất trung điểm)
Vậy x=5dm.
bài 24
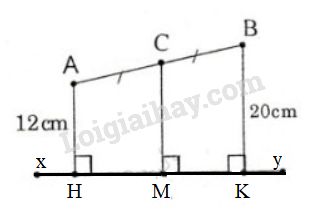
Kẻ AH,CM,BK vuông góc với xy (H,M,K là chân đường vuông góc).
⇒AH//CM//BK(cùng vuông góc với đường thẳng xy)
⇒ Tứ giác ABKHlà hình thang (dấu hiệu nhận biết hình thang)
Xét hình thang ABKHcó: AC=CB (giả thiết)
CM//AH//BK (chứng minh trên)
Suy ra MH=MK (Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai)
⇒CM là đường trung bình của hình thang ABKH (dấu hiệu nhận biết đường trung bình của hình thang)
⇒
Bài 25
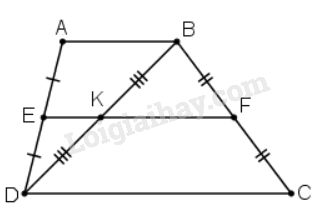
- Xét ΔABD có: E,K lần lượt là trung điểm của AD,BD (giả thiết)
⇒EK là đường trung bình của ΔABD (dấu hiệu nhận biết đường trung bình của tam giác)
⇒EK//AB(tính chất đường trung bình của tam giác) (1)
- Xét ΔDBC có: F,K lần lượt là trung điểm của BC,BD (giả thiết)
⇒FK là đường trung bình của ΔDBC (dấu hiệu nhận biết đường trung bình của tam giác)
⇒FK//DC (tính chất đường trung bình của tam giác)
Mặt khác, AB//DC (vì ABCDlà hình thang) nên suy ra FK//AB (2)
Từ (1) và (2) ta có qua điểm K không thuộc AB có hai đường thẳng EK và FK cùng //AB nên theo tiên đề Ơ-clit thì ba điểm E,K,F thẳng hàng .