vẽ đò thị h.số
y=2x-1 nếu x >1 y=2-x nếu x<1 . xác định m để y=m cắt đồ thị hàm số tại 2 điểm phân biệt. Tìm giao điểm của 2 đồ thị trên
Một điểm M thuộc parabol (P): y 2 = x. Nếu khoảng cách từ M đến tiêu điểm F của (P) bằng 1 thì hoành độ của điểm M bằng bao nhiêu?
A. 3/4
B. 3 /2
C. 3
D. 3
Đáp án: A
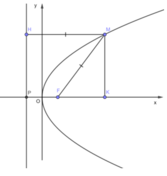
(P): y 2 = x ⇒ p = 1/2
Ta có:
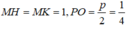
Hoành độ của điểm M chính là độ dài đoạn OK
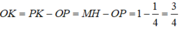
Nếu hai đường thẳng y=2x+3+m và y=x+6-m cắt nhau tại một điểm trên trục hoành thì hoành độ giao điểm đó là x= ....
Trục hoành là y = 0, tìm giao điểm của trục hoành với một trong hai đường, chẳng hạn : y = x + 6 - m
PT hoành độ giao điểm : x + 6 - m = 0 <=> x = m - 6
Phương trình hoành độ giao điểm của y = 2x + 3 + m với y = 0 (trục Ox) :
2x + 3 + m = 0
Thay x = m - 6 vào phương trình trên :
2(m - 6) + 3 + m = 0
<=> 3m = 9
<=> m = 3
Vậy m cần tìm là m = 3
=>x=3-2.3=-3
Cho trước tam giác ABC , và giả sử điểm M thoả mãn đẳng thức \(x\overrightarrow{MA}+y\overrightarrow{MB}+z\overrightarrow{MC}=\overrightarrow{0}\) ( trong đó x,y,z là số thực ). Hãy chọn khẳng định đúng
A. Nếu x,y,z \(\ne\)0 thì tồn tại duy nhất điểm M thoả mãn đẳng thức trên
B. Nếu x+y+z=0 thì tồn tại duy nhất điểm M thoả mãn đẳng thức trên
C. Nếu ít nhất 1 trong 3 số x,y,z \(\ne\) thì tồn tại duy nhất điểm M thoả mãn đẳng thức trên
D. Nếu cả 3 số x,y,z \(\ne\)0 thì tồn tại duy nhất điểm M thoả mãn đẳng thức trên
Tính theo m khoảng cách giữa điểm cực đại và điểm cực tiểu ( nếu có) của đồ thị hàm số: y = 1 3 x 3 - m x 2 - x + m + 1
A. 2 3 ( m 2 + 1 ) ( 4 m 4 + 5 m 2 + 9 )
B. 4 9 ( 2 m 2 + 1 ) ( 4 m 4 + 8 m 2 + 13 )
C. 2 3 ( m 2 + 1 ) ( 4 m 4 + 8 m 2 + 13 )
D. ( 4 m 2 + 4 ) ( 4 m 4 + 8 m 2 + 10 )
CÁC BẠN ƠI NHẬN XÉT GIÙM MÌNH VỚI:
NẾU MÌNH MUỐN CHỨNG MINH 3 ĐIỂM ( A,B,C)THẲNG HÀNG THÌ MÌNH CHỨNG MINH ĐIỂM A LÀ TRUNG ĐIỂM CỦA BC ĐƯỢC KO Ạ. (NẾU KO ĐƯỢC THÌ TẠI SAO?)
Bạn ko thể chứng minh như thế đc nhỡ may B, C cũng ko thẳng hàng thì sao
nếu 2 đường thẳng y=2x+3+m và y=x+6-m cắt nhau tại 1 điểm trên trục hoành thì hoành độ giao điểm đó là ...
Trục hoành là y = 0, tìm giao điểm của trục hoành với một trong hai đường, chẳng hạn :
y = x + 6 - m
PT hoành độ giao điểm :
x + 6 - m = 0 <=> x = m - 6
Phương trình hoành độ giao điểm của : y = 2x + 3 + m với y = 0 (trục Ox) :
2x + 3 + m = 0
Thay x = m - 6 vào phương trình trên :
2(m - 6) + 3 + m = 0
<=> 3m = 9
<=> m = 3
****
Nếu 2 đường thẳng y=2x+3+m và y=x+6-m cắt nhau tại một điểm trên trục hoành thì hoành độ giao điểm đó là
Trục hoành là y = 0, tìm giao điểm của trục hoành với một trong hai đường, chẳng hạn :
y = x + 6 - m
PT hoành độ giao điểm :
x + 6 - m = 0 <=> x = m - 6
Phương trình hoành độ giao điểm của : y = 2x + 3 + m với y = 0 (trục Ox) :
2x + 3 + m = 0
Thay x = m - 6 vào phương trình trên :
2(m - 6) + 3 + m = 0
<=> 3m = 9
<=> m = 3
****
bài này chỉ vừa tính đc m=3,thay vào ta có hoành độ giao điểm x=-3
cho hpt mx+2my và x+(m+1)y=2
a,cmr nếu hệ có nghiệm duy nhất (x,y) thì điểm M(x,y)luôn thuộc 1 đường thẳng cố định khi m thay đổi
b,xác định m để điểm M thuộc góc vuông phần tư thứ nhất
Nếu hai đường thẳng y = 2x+3+m và y=x+6-m cắt nhau tại một điểm trên trục hoành thì hoành độ giao điểm đó là
3 + m = 6- m => m = 3/2 => b =2+m = 2 +3/2 =7/2
=> Giao điểm A( 0; 7/2 )
.
