Viết phương trình mặt cầu (S) biết (S) qua bốn điểm A ( 1 ; 2 ; - 4 ) ; B ( 1 ; - 3 ; 1 ) ; C ( 2 ; 2 ; 3 ) v à D ( 1 ; 0 ; 4 ) .
A. x + 2 2 + y - 1 2 + z 2 = 26
B. x - 2 2 + y + 1 2 + z 2 = 13
C. x + 2 2 + y + 1 2 + z 2 = 52
D. Đáp án khác
Những câu hỏi liên quan
Viết phương trình mặt cầu (S) biết (S) qua bốn điểm
A
(
1
;
2
;
-
4
)
;
B
(
1
;
-
3
;
1
)
;
C
(
2
;
2
;
3
)
v
à
D
(
1
;
0
;
4
)
.
A.
x
+...
Đọc tiếp
Viết phương trình mặt cầu (S) biết (S) qua bốn điểm A ( 1 ; 2 ; - 4 ) ; B ( 1 ; - 3 ; 1 ) ; C ( 2 ; 2 ; 3 ) v à D ( 1 ; 0 ; 4 ) .
A. x + 2 2 + y - 1 2 + z 2 = 26
B. x - 2 2 + y + 1 2 + z 2 = 13
C. x + 2 2 + y + 1 2 + z 2 = 52
D. Đáp án khác
Chọn A.
Gọi phương trình mặt cầu (S): x2 + y2 + z2 - 2ax - 2by - 2cz + d = 0, (a2 + b2 + c2 - d > 0)
có tâm I (a;b;c) và bán kính 
Do A(1;2;-4) ∈ (S)nên: 12 + 22 + (-42 – 2.a.1 – 2b .2 - 2c.(-4) + d = 0 hay -2a - 4b + 8c + d = -21 (1)
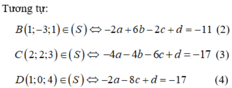
Giải hệ (1), (2), (3), (4) ta có: a = -2; b = 1; c = 0; d = -21, suy ra phương trình mặt cầu (S) :
(x + 2)2 + (y - 1)2 + z2 = 26.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho mặt cầu (S) đi qua bốn điểm O, A(-4;0;0), B(0;2;0), C(0;0;4). Phương trình của mặt cầu (S) là: A.
x
2
+
y
2
+
z
2
+ 2x - y - 2z 0 B.
x
2
+
y...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) đi qua bốn điểm O, A(-4;0;0), B(0;2;0), C(0;0;4). Phương trình của mặt cầu (S) là:
A. x 2 + y 2 + z 2 + 2x - y - 2z = 0
B. x 2 + y 2 + z 2 + 4x + 2y - 4z = 0
C. x 2 + y 2 + z 2 + 4x - 2y + 4z = 0S
D. x 2 + y 2 + z 2 + 4x - 2y - 4z = 0
Đáp án D
Phương trình tổng quát của mặt cầu (S) có dạng x 2 + y 2 + z 2 - 2ax - 2by - 2cz + d = 0 với a 2 + b 2 + c 2 - d > 0
Ta có: O(0; 0; 0) ∈ (S) ⇔ d = 0
A(-4; 0; 0) ∈ (S) ⇔ ( - 4 ) 2 + 0 2 + 0 2 - 2a.(-4) - 0 - 0 + 0 = 0 ⇔ a = -2
B(0; 2; 0) ∈ (S) ⇔ 0 2 + 2 2 + 0 2 - 0 - 2b.2 - 0 + 0 = 0 ⇔ b = 1
C(0; 0; 4) ∈ (S) ⇔ 0 2 + 0 2 + 4 2 - 0 - 0 - 2c.4 - 0 = 0 ⇔ c = 2
Vậy phương trình tổng quát của mặt cầu (S) là: x 2 + y 2 + z 2 + 4x -2y - 4z = 0
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho mặt cầu (S) đi qua bốn điểm O, A(4;0;0), B(0;-2;0), C(0;0;2). Phương trình của mặt cầu (S) là: A.
(
x
-
1
)
2
+
(
y
+
...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) đi qua bốn điểm O, A(4;0;0), B(0;-2;0), C(0;0;2). Phương trình của mặt cầu (S) là:
A. ( x - 1 ) 2 + ( y + 1 ) 2 + ( z - 1 ) 2 = 6
B. ( x - 2 ) 2 + ( y + 1 ) 2 + ( z - 1 ) 2 = 24
C. ( x - 4 ) 2 + ( y + 2 ) 2 + ( z + 2 ) 2 = 24
D. ( x + 2 ) 2 + ( y - 1 ) 2 + ( z + 1 ) 2 = 6
Trong không gian với hệ tọa độ Oxyz, mặt cầu (S) qua bốn điểm A(3;3;0), B(3;0;3), C(0;3;3), D(3;3;3). Phương trình mặt cầu (S) là
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, mặt cầu (S) qua bốn điểm A(3;3;0), B(3;0;3), C(0;3;3), D(3;3;3). Phương trình mặt cầu (S) là
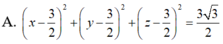
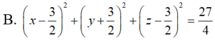
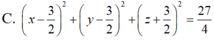
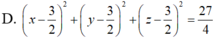
Trong không gian Oxyz, cho bốn điểm \(A\left(6;-2;3\right),B\left(0;1;6\right),C\left(2;0;-1\right),D\left(4;1;0\right)\). Gọi (S) là mặt cầu đi qua 4 điểm A, B, C, D. Hãy viết phương trình mặt phẳng tiếp xúc với mặt cầu (S) tại điểm A ?
Trong không gian Oxyz, cho bốn điểm \(A\left(1;0;0\right),B\left(0;1;0\right),C\left(0;0;1\right),D\left(1;1;0\right)\)
a) Viết phương trình mặt cầu (S) đi qua bốn điểm A, B, C, D
b) Xác định tọa đọ tâm và bán kính của đường tròn là giao tuyến của mặt cầu (S) với mặt phẳng (ACD)
Trong không gian Oxyz, cho 4 điểm Aleft(2;4;-1right),Bleft(1;4;-1right),Cleft(1;4;3right),Dleft(2;2;-1right)
a) Chứng minh rằng các đường thẳng AB, AC, AD vuông góc với nhau từng đôi một
b) Viết phương trình tham số của đường vuông góc chung Delta của hai đường thẳng AB và CD
c) Viết phương trình mặt cầu (S) đi qua bốn điểm A, B, C, D
d) Viết phương trình mặt phẳng left(alpharight) tiếp xúc với mặt cầu (S) và song song với mặt phẳng (ABD)
Đọc tiếp
Trong không gian Oxyz, cho 4 điểm \(A\left(2;4;-1\right),B\left(1;4;-1\right),C\left(1;4;3\right),D\left(2;2;-1\right)\)
a) Chứng minh rằng các đường thẳng AB, AC, AD vuông góc với nhau từng đôi một
b) Viết phương trình tham số của đường vuông góc chung \(\Delta\) của hai đường thẳng AB và CD
c) Viết phương trình mặt cầu (S) đi qua bốn điểm A, B, C, D
d) Viết phương trình mặt phẳng \(\left(\alpha\right)\) tiếp xúc với mặt cầu (S) và song song với mặt phẳng (ABD)
Viết phương trình mặt cầu (S) đi qua điểm A(5;-2;1) và có tâm C(3;-3;1) A.
x
+
3
2
+
y
-
3
2
+
z
+
1
2
5
B.
x...
Đọc tiếp
Viết phương trình mặt cầu (S) đi qua điểm A(5;-2;1) và có tâm C(3;-3;1)
A. x + 3 2 + y - 3 2 + z + 1 2 = 5
B. x - 3 2 + y + 3 2 + z + 1 2 = 5
C. x - 3 2 + y + 3 2 + z - 1 2 = 5
D. x - 3 2 + y + 3 2 + z - 1 2 = 5
Trong không gian Oxyz, cho mặt cầu (S) có phương trình
x
2
+
y
2
+
z
2
1. Viết phương trình mặt phẳng (P) đi qua và tiếp xúc với (S) A.
3
x + 4z - 2 0 B.
3
y + z - 2 0 C. y +
3
z 0 D. x +
3
y + z - 2 0
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) có phương trình
x
2
+
y
2
+
z
2
= 1. Viết phương trình mặt phẳng (P) đi qua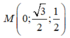 
và tiếp xúc với (S)
A. 3 x + 4z - 2 = 0
B. 3 y + z - 2 = 0
C. y + 3 z = 0
D. x + 3 y + z - 2 = 0
