Cho đồ thị hàm số y = f(x). Diện tích hình phẳng ( phần gạch sọc ) là:
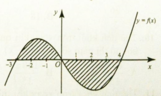
A. ∫ - 3 4 f x d x
B. ∫ - 3 1 f x d x + ∫ 1 4 f x d x
C. ∫ - 3 0 f x d x + ∫ 0 4 - f x d x
D. ∫ - 3 0 f x d x + ∫ 0 4 f x d x
Những câu hỏi liên quan
Cho đồ thị hàm số y f(x). Diện tích hình phẳng (phần gạch trong hình) là:
Đọc tiếp
Cho đồ thị hàm số y = f(x). Diện tích hình phẳng (phần gạch trong hình) là:
Cho đồ thị hàm số y f(x). Diện tích hình phẳng (phần gạch trong hình) là: A.
∫
0
−
3
f
x
d
x
+
∫
0
4...
Đọc tiếp
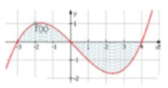
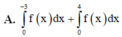
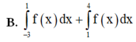
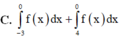
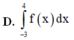
Cho đồ thị hàm số y = f(x). Diện tích hình phẳng (phần gạch trong hình) là:
A. ∫ 0 − 3 f x d x + ∫ 0 4 f x d x
B. ∫ − 3 1 f x d x + ∫ 1 4 f x d x
C. ∫ − 3 0 f x d x + ∫ 4 0 f x d x
D. ∫ − 3 4 f x d x
Đáp án C
- Vì đồ thị của hàm số f(x) cắt Ox tại điểm có hoành độ bằng 0 nên:
- Diện tích phần gạch trên hình là:
Đúng 0
Bình luận (0)
Hình phẳng (H) được giới hạn bởi đồ thị của hai hàm số đa thức bậc bốn yf(x) và yg(x). Biết rằng đồ thị của hai hàm số này cắt nhau tại đúng ba điểm phân biệt có hoành độ lần lượt là −3;−1;2. Diện tích của hình phẳng (H) (phần gạch sọc trên hình vẽ bên) gần nhất với kết quả nào dưới đây? A.3,11 B. 2,45 C. 3,21 D. 2,95
Đọc tiếp
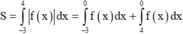
Hình phẳng (H) được giới hạn bởi đồ thị của hai hàm số đa thức bậc bốn y=f(x) và y=g(x). Biết rằng đồ thị của hai hàm số này cắt nhau tại đúng ba điểm phân biệt có hoành độ lần lượt là −3;−1;2. Diện tích của hình phẳng (H) (phần gạch sọc trên hình vẽ bên) gần nhất với kết quả nào dưới đây?
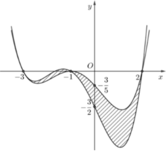
A.3,11
B. 2,45
C. 3,21
D. 2,95
Cho đồ thị hàm số yf(x) Diện tích hình phẳng (phần có dấu gạch trong hình) là
Đọc tiếp
Cho đồ thị hàm số y=f(x) Diện tích hình phẳng (phần có dấu gạch trong hình) là
Cho đồ thị hàm số y f(x) Diện tích hình phẳng (phần có dấu gạch trong hình) là: A.
S
∫
-
3
0
f
(
x
)
d
x
-
∫
0
4
f
(
x
)...
Đọc tiếp
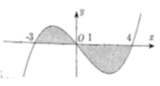
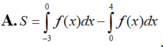
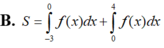
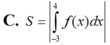
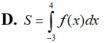
Cho đồ thị hàm số y = f(x) Diện tích hình phẳng (phần có dấu gạch trong hình) là:
A. S = ∫ - 3 0 f ( x ) d x - ∫ 0 4 f ( x ) d x
B. S = ∫ - 3 0 f ( x ) d x + ∫ 0 4 f ( x ) d x
C. S = ∫ - 3 4 f ( x ) d x
D. S = ∫ - 3 4 f ( x ) d x
Cho đồ thị hàm số y f(x). Diện tích hình phẳng (phần có đánh dấu gạch trong hình) là: A.
∫
-
3
0
f
x
d
x
+
∫
4
0
f
x
d
x
B.
∫
-
3
1
f
x
d...
Đọc tiếp
Cho đồ thị hàm số y = f(x). Diện tích hình phẳng (phần có đánh dấu gạch trong hình) là:
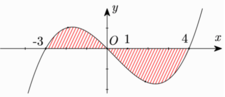
A. ∫ - 3 0 f x d x + ∫ 4 0 f x d x
B. ∫ - 3 1 f x d x + ∫ 1 4 f x d x
C. ∫ 0 - 3 f x d x + ∫ 0 4 f x d x
D. ∫ - 3 4 f x d x
Cho đồ thị hàm số
y
f
(
x
)
.
Diện tích hình phẳng (phần có đánh dấu gạch trong hình) là: A.
∫
-
3
0
f
x
d
x
+
∫
4
0
f
x
d
x
B.
∫
-...
Đọc tiếp
Cho đồ thị hàm số y = f ( x ) . Diện tích hình phẳng (phần có đánh dấu gạch trong hình) là:
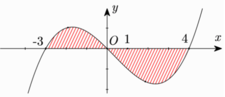
A. ∫ - 3 0 f x d x + ∫ 4 0 f x d x
B. ∫ - 3 1 f x d x + ∫ 1 4 f x d x
C. ∫ 0 - 3 f x d x + ∫ 0 4 f x d x
D. ∫ - 3 4 f x d x
Biết đồ thị hàm số
f
(
x
)
a
x
4
+
b
x
2
+
c
cắt trục hoành tại 4 điểm phân biệt. Gọi
S...
Đọc tiếp
Biết đồ thị hàm số f ( x ) = a x 4 + b x 2 + c cắt trục hoành tại 4 điểm phân biệt. Gọi S 1 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f ( x ) nằm dưới trục hoành. Gọi S 2 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f ( x ) nằm phía trên trục hoành. Cho biết 5 b 2 = 36 a c . Tính tỉ số S 1 S 2
A. S 1 S 2 = 2 .
B. S 1 S 2 = 1 4 .
C. S 1 S 2 = 1 2 .
D. S 1 S 2 = 1 .
Đáp án D
Phương trình hoành độ giao điểm của đồ thị f ( x ) và Ox: a x 4 + b x 2 + c = 0 .
Để phương trình có bốn nghiệm
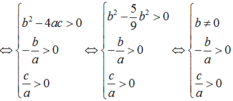
Gọi x 1 , x 2 , x 3 , x 4 lần lượt là bốn nghiệm của phương trình a x 4 + b x 2 + c = 0 và x 1 < x 2 < x 3 < x 4 . Không mất tính tổng quát, giả sử a > 0 .
Khi đó
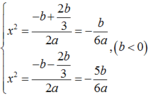
Suy ra x 1 = - - 5 b 6 a ; x 2 = - - b 6 a ; x 3 = - b 6 a ; x 4 = - b 6 a .
Do đồ thị hàm số f ( x ) nhận trục tung làm trục đối xứng nên ta có:
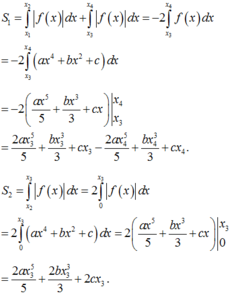
Suy ra
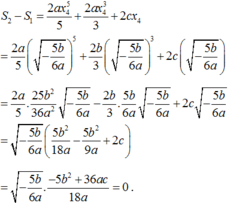
Vậy S 1 = S 2 hay S 1 S 2 = 1 .
Đúng 0
Bình luận (0)
Cho hàm số y f(x) liên tục trên
ℝ
và hàm số
y
g
x
x
2
f
x
3
có đồ thị trên đoạn [-1;3] như hình vẽ. Biết miền hình phẳng được tô sọc kẻ có diện tích S 6. Tính tích phân
I
∫
1
27
f
x
d
x
.
A. I 2...
Đọc tiếp
Cho hàm số y = f(x) liên tục trên ℝ và hàm số y = g x = x 2 f x 3 có đồ thị trên đoạn [-1;3] như hình vẽ. Biết miền hình phẳng được tô sọc kẻ có diện tích S = 6. Tính tích phân I = ∫ 1 27 f x d x .
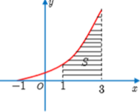
A. I = 2.
B. I = 12.
C. I = 24.
D. I = 18.
