Họ nguyên hàm của hàm số f(x)=4x(1+lnx) là
Những câu hỏi liên quan
Họ nguyên hàm của hàm số f(x)4x(1+lnx) là A.
2
x
2
ln
x
+
3
x
2
B.
2
x
2
ln
x
+
x
2
C.
2
x
2
ln
x...
Đọc tiếp
Họ nguyên hàm của hàm số f(x)=4x(1+lnx) là
A. 2 x 2 ln x + 3 x 2
B. 2 x 2 ln x + x 2
C. 2 x 2 ln x + 3 x 2 + C
D. 2 x 2 ln x + x 2 + C
Họ các nguyên hàm của hàm số f(x)(2x+1)lnx là A.
x
2
+
x
ln
x
-
x
2
2
+
x
+
C
B.
x
2...
Đọc tiếp
Họ các nguyên hàm của hàm số f(x)=(2x+1)lnx là
A. x 2 + x ln x - x 2 2 + x + C
B. x 2 + x ln x - x 2 2 - x + C
C. x 2 + 1 ln x - x 2 2 - x + C
D. 2 ln x + 1 2 + C
Họ nguyên hàm F(x) của hàm số
f
(
x
)
x
lnx
là A.
F
(
x
)
x
2
2
lnx
-...
Đọc tiếp
Họ nguyên hàm F(x) của hàm số f ( x ) = x lnx là
A. F ( x ) = x 2 2 lnx - x 2 2 + C
B. F ( x ) = x 2 2 lnx - x 2 4 + C
C. F ( x ) = x 2 2 lnx + x 2 2 + C
D. F ( x ) = x 2 2 lnx + x 2 4 + C
Họ nguyên hàm của hàm
f
(
x
)
e
2
x
-
1
x
+
ln
x
(
x
0
)
là
Đọc tiếp
Họ nguyên hàm của hàm f ( x ) = e 2 x - 1 x + ln x ( x > 0 ) là
Cho F(x)
1
2
x
2
là 1 nguyên hàm của hàm số
f
(
x
)
x
. Tìm nguyên hàm của hàm số f(x)lnx
Đọc tiếp
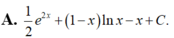
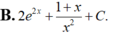
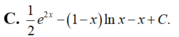
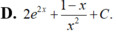
Cho F(x) = 1 2 x 2 là 1 nguyên hàm của hàm số f ( x ) x . Tìm nguyên hàm của hàm số f'(x)lnx
Cho
F
(
x
)
-
1
3
x
3
là một nguyên hàm của hàm số
f
(
x
)
x
Tìm nguyên hàm của hàm số f(x)lnx
Đọc tiếp
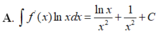
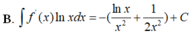
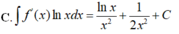
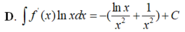
Cho F ( x ) = - 1 3 x 3 là một nguyên hàm của hàm số f ( x ) x Tìm nguyên hàm của hàm số f'(x)lnx
Họ nguyên hàm của hàm số f(x) 4x(1+ln x) là A.
2
x
2
ln
x
+
3
x
2
B.
2
x
2
ln
x
+
x
2
C.
2
x...
Đọc tiếp
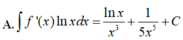
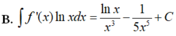
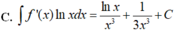
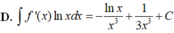
Họ nguyên hàm của hàm số f(x) = 4x(1+ln x) là
A. 2 x 2 ln x + 3 x 2
B. 2 x 2 ln x + x 2
C. 2 x 2 ln x + 3 x 2 + C
D. 2 x 2 ln x + x 2 + C
Đáp án D
Phương pháp:
Cách 1: Sử dụng công thức tính nguyên hàm của 1 tổng.
Cách 2: Đạo hàm từng đáp án của đề bài, kết quả nào ra đúng f(x) thì đó là đáp án đúng
Cách giải:
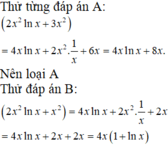
⇒ 2 x 2 ln x + x 2 là một nguyên hàm của hàm số f x = 4 x 1 + ln x
⇒ Họ nguyên hàm của hàm số f x = 4 x 1 + ln x là 2 x 2 ln x + x 2 + C
Đúng 0
Bình luận (0)
Cho
F
x
-
1
3
x
3
là một nguyên hàm của hàm số
f
x
x
. Tìm nguyên hàm của hàm số f(x)lnx. A.
∫
f
x
d
x...
Đọc tiếp
Cho F x = - 1 3 x 3 là một nguyên hàm của hàm số f x x . Tìm nguyên hàm của hàm số f'(x)lnx.
A. ∫ f ' x d x = ln x x 3 + 1 3 x 3 + C
B. ∫ f ' x d x = - ln x x 3 + 1 3 x 3 + C
C. ∫ f ' x d x = - ln x x 3 + 1 5 x 3 + C
D. ∫ f ' x d x = ln x x 3 + 1 5 x 3 + C
Cho
F
x
−
1
3
x
3
là một nguyên hàm của hàm số
f
x
x
.
Tìm nguyên hàm của hàm số f (x).lnx A.
∫
f...
Đọc tiếp
Cho F x = − 1 3 x 3 là một nguyên hàm của hàm số f x x . Tìm nguyên hàm của hàm số f '(x).lnx
A. ∫ f ' x lnxdx = lnx x 3 + 1 5 x 5 + C .
B. ∫ f ' x lnxdx = lnx x 3 − 1 5 x 5 + C .
C. ∫ f ' x lnxdx = lnx x 3 + 1 3 x 3 + C .
D. ∫ f ' x lnxdx = − lnx x 3 + 1 3 x 3 + C .
Đáp án C
F x = − 1 3 x 3 là một nguyên hàm của f x x nên
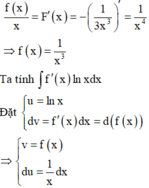
Áp dụng công thức nguyên hàm từng phần ta có
∫ f ' x lnxdx = ∫ lnxd f x = lnx . f x − ∫ f x x dx = lnx x 3 + 1 3 x 3 + C
Đúng 0
Bình luận (0)